# --- Configuración del entorno ---
# Cargamos las librerías necesarias
pacman::p_load(
tidyverse, # Manipulación y gráficos (ggplot2, dplyr...)
haven, # Leer SPSS
psych, # Estadísticos descriptivos
car, # Diagnósticos de regresión (VIF, Durbin-Watson)
lmtest, # Tests adicionales
patchwork, # Composición de gráficos
Hmisc # Correlaciones con p-valores
)7 Regresión lineal múltiple
Caso práctico: Rendimiento académico en los institutos de Chicago
7.1 Introducción
La regresión lineal múltiple es la “navaja suiza” del análisis de datos. Nos permite no solo predecir el futuro (¿qué nota sacará este alumno?), sino también explicar el presente (¿qué factores influyen más en el éxito académico?).
En este caso práctico, analizaremos datos reales de 82 institutos de Chicago. Nuestro objetivo es entender qué variables explican mejor el éxito de los alumnos en la prueba de selectividad.
La pregunta de investigación:
¿Qué explica que los alumnos de distintos institutos tengan un nivel de éxito diferente?
Nuestras variables:
- Dependiente (\(Y\)):
selectivo(% de aprobados en selectividad). - Independientes (\(X\)):
asistencia: % de asistencia regular.tamclase: # medio de alumnos en la clase.extranjero: % de alumnos extranjeros.rentabaja: % de alumnos de hogares de renta baja.
7.2 1. Análisis exploratorio: La relación lineal
Antes de modelizar, podemos verificar si existe una relación lineal básica entre nuestras variables. No es un requisito necesario, pero si nos ayuda a comprender la posible relación entre las variables. Del mismo modo, un análisis descriptivo siempre sería bienvenido.
summary(data) id instituto tipo asistencia
Min. : 1.00 Length:82 Length:82 Min. :73.70
1st Qu.:21.25 Class :character Class :character 1st Qu.:83.60
Median :41.50 Mode :character Mode :character Median :86.00
Mean :41.50 Mean :86.57
3rd Qu.:61.75 3rd Qu.:90.20
Max. :82.00 Max. :95.80
NA's :1
rentabaja extranjero selectivo tamclase
Min. :23.10 Min. : 0.00 Min. : 0.00 Min. : 4.80
1st Qu.:77.85 1st Qu.: 0.00 1st Qu.: 15.20 1st Qu.:15.45
Median :85.65 Median : 0.35 Median : 23.20 Median :17.90
Mean :80.93 Mean : 4.17 Mean : 30.16 Mean :17.86
3rd Qu.:90.12 3rd Qu.: 7.00 3rd Qu.: 38.90 3rd Qu.:21.18
Max. :98.60 Max. :22.30 Max. :100.00 Max. :27.20
NA's :1 # Matriz de correlaciones
# Usamos Hmisc para ver coeficientes y significación
rcorr(as.matrix(select(data, selectivo, asistencia, rentabaja, extranjero, tamclase))) selectivo asistencia rentabaja extranjero tamclase
selectivo 1.00 0.72 -0.71 -0.14 0.50
asistencia 0.72 1.00 -0.52 -0.01 0.59
rentabaja -0.71 -0.52 1.00 0.10 -0.43
extranjero -0.14 -0.01 0.10 1.00 0.07
tamclase 0.50 0.59 -0.43 0.07 1.00
n
selectivo asistencia rentabaja extranjero tamclase
selectivo 81 80 81 81 81
asistencia 80 81 81 81 81
rentabaja 81 81 82 82 82
extranjero 81 81 82 82 82
tamclase 81 81 82 82 82
P
selectivo asistencia rentabaja extranjero tamclase
selectivo 0.0000 0.0000 0.2062 0.0000
asistencia 0.0000 0.0000 0.9601 0.0000
rentabaja 0.0000 0.0000 0.3555 0.0000
extranjero 0.2062 0.9601 0.3555 0.5222
tamclase 0.0000 0.0000 0.0000 0.5222 # Visualización rápida
pairs(select(data, selectivo, asistencia, rentabaja, extranjero, tamclase),
main = "Matriz de dispersión", pch = 19, col = "steelblue")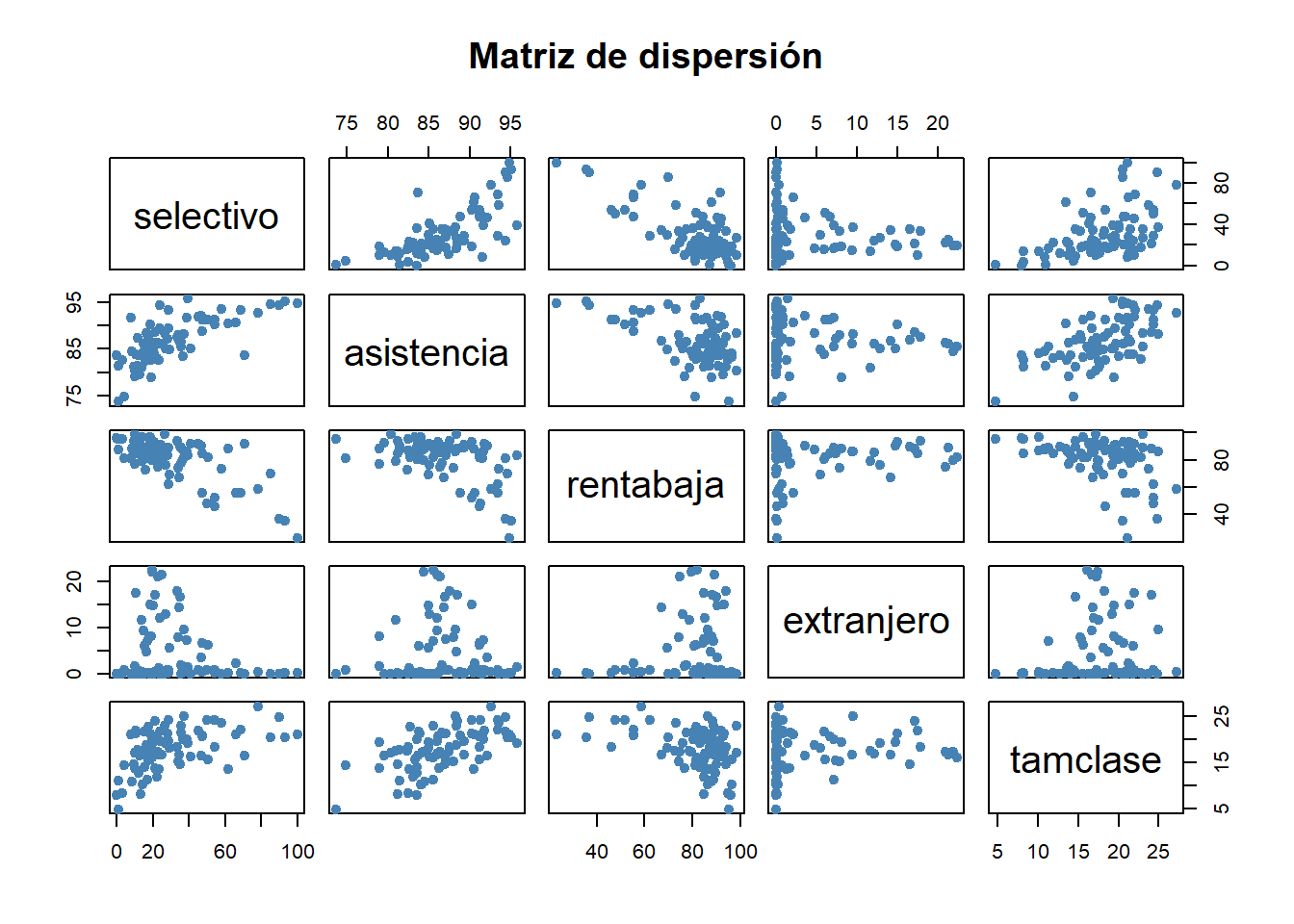
Interpretación: Observamos correlaciones fuertes. Por ejemplo, asistencia tiene una correlación positiva muy alta con selectivo, mientras que rentabaja tiene una correlación negativa fuerte. Esto nos da “luz verde” para construir el modelo.
7.3 2. Estimación del modelo de regresión
Vamos a construir nuestro modelo utilizando el método de Mínimos Cuadrados Ordinarios (MCO).
# Construcción del modelo
modelo1 <- lm(selectivo ~ asistencia + rentabaja + extranjero + tamclase, data = data)
# Resumen estadístico
summary(modelo1)
Call:
lm(formula = selectivo ~ asistencia + rentabaja + extranjero +
tamclase, data = data)
Residuals:
Min 1Q Median 3Q Max
-34.845 -6.649 -1.301 6.234 52.897
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -110.5677 37.5578 -2.944 0.00431 **
asistencia 2.2045 0.4106 5.370 8.51e-07 ***
rentabaja -0.6517 0.1136 -5.739 1.90e-07 ***
extranjero -0.2593 0.2300 -1.127 0.26316
tamclase 0.2119 0.4162 0.509 0.61222
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.86 on 75 degrees of freedom
(2 observations deleted due to missingness)
Multiple R-squared: 0.6839, Adjusted R-squared: 0.6671
F-statistic: 40.57 on 4 and 75 DF, p-value: < 2.2e-167.3.1 Interpretación de los resultados
- Bondad de ajuste (\(R^2\)): El valor de R-squared nos dice qué porcentaje de la variabilidad de la nota de selectividad explicamos. Un valor cercano a 1 es excelente.
- Significatividad del modelo (F-statistic): Si el p-valor es < 0.05, el modelo en su conjunto funciona mejor que el azar.
- Coeficientes (\(B\)):
- Fíjate en la columna
Estimate. - Por ejemplo, si el coeficiente de
asistenciaes positivo, significa que a mayor asistencia, mayor nota. - Si el
Pr(>|t|)es < 0.05, esa variable específica es relevante para el modelo.
- Fíjate en la columna
7.4 3. Importancia relativa de las variables (Coeficientes Beta)
Los coeficientes anteriores (\(B\)) dependen de las unidades (porcentajes, número de alumnos…). Para saber qué variable es “más importante” o tiene más fuerza, necesitamos los coeficientes estandarizados (Beta).
# Calculamos los coeficientes estandarizados manualmente
# (Escalamos los datos y re-hacemos el modelo)
data_scaled <- as.data.frame(scale(select(data, selectivo, asistencia, rentabaja, extranjero, tamclase)))
modelo_beta <- lm(selectivo ~ ., data = data_scaled)
# Mostramos los coeficientes Beta ordenados por impacto absoluto
coef_beta <- coef(modelo_beta)[-1] # Quitamos el intercepto
sort(abs(coef_beta), decreasing = TRUE)asistencia rentabaja extranjero tamclase
0.46180645 0.44316069 0.07528587 0.04249172 Interpretación: La variable con el valor absoluto más alto es la que tiene mayor peso en la predicción. Esto responde a la pregunta de gestión: “¿Dónde debo invertir mis recursos para mejorar o incrementar el éxito de los alumnos?”.
7.5 4. Validación de supuestos en el modelo, análisis de los residuos
No podemos confiar en el modelo hasta que no analicemos su “basura” (los residuos). Si el modelo es bueno, los residuos deben ser ruido aleatorio. Si vemos patrones, tenemos problemas.
7.5.1 4.1. Detección de outliers (Distancia de De Cook)
¿Hay algún instituto cuyo comportamiento sea tan extraño que esté distorsionando todo el análisis?
# Cálculo de la distancia de De Cook
cooksd <- cooks.distance(modelo1)
# Gráfico
plot(cooksd, pch="*", cex=2, main="Distancia de De Cook (Outliers)", ylab="Distancia de De Cook")
abline(h = 4/nrow(data), col="red") # Umbral de referencia (4/n)
text(x=1:length(cooksd)+1, y=cooksd, labels=ifelse(cooksd>4/nrow(data),names(cooksd),""), col="red")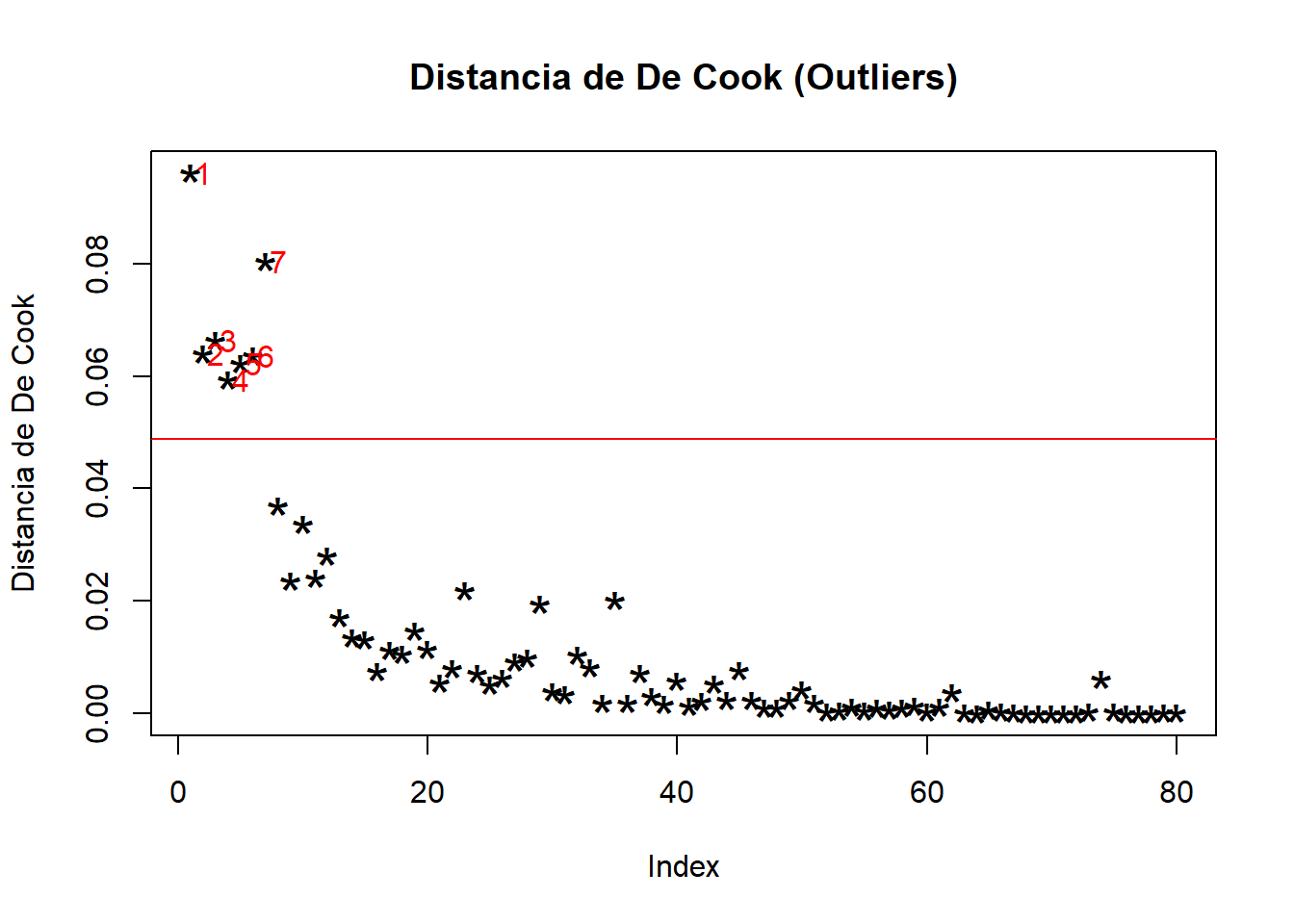
7.5.2 4.2. Supuesto de linealidad
Comprobamos que la relación global sea lineal. Buscamos una nube aleatoria sin formas de “U”.
# Preparamos datos para ggplot
df_diag <- data.frame(
predichos = fitted(modelo1),
residuos_std = rstandard(modelo1)
)
ggplot(df_diag, aes(x = predichos, y = residuos_std)) +
geom_point(color = "steelblue", alpha = 0.6) +
geom_hline(yintercept = 0, linetype = "dashed") +
geom_smooth(method = "loess", se = FALSE, color = "red", linetype="dotted") +
labs(title = "Linealidad: Predichos vs. Residuos",
subtitle = "Buscamos una nube sin patrones curvos",
x = "Valores Predichos", y = "Residuos Estandarizados") +
theme_minimal()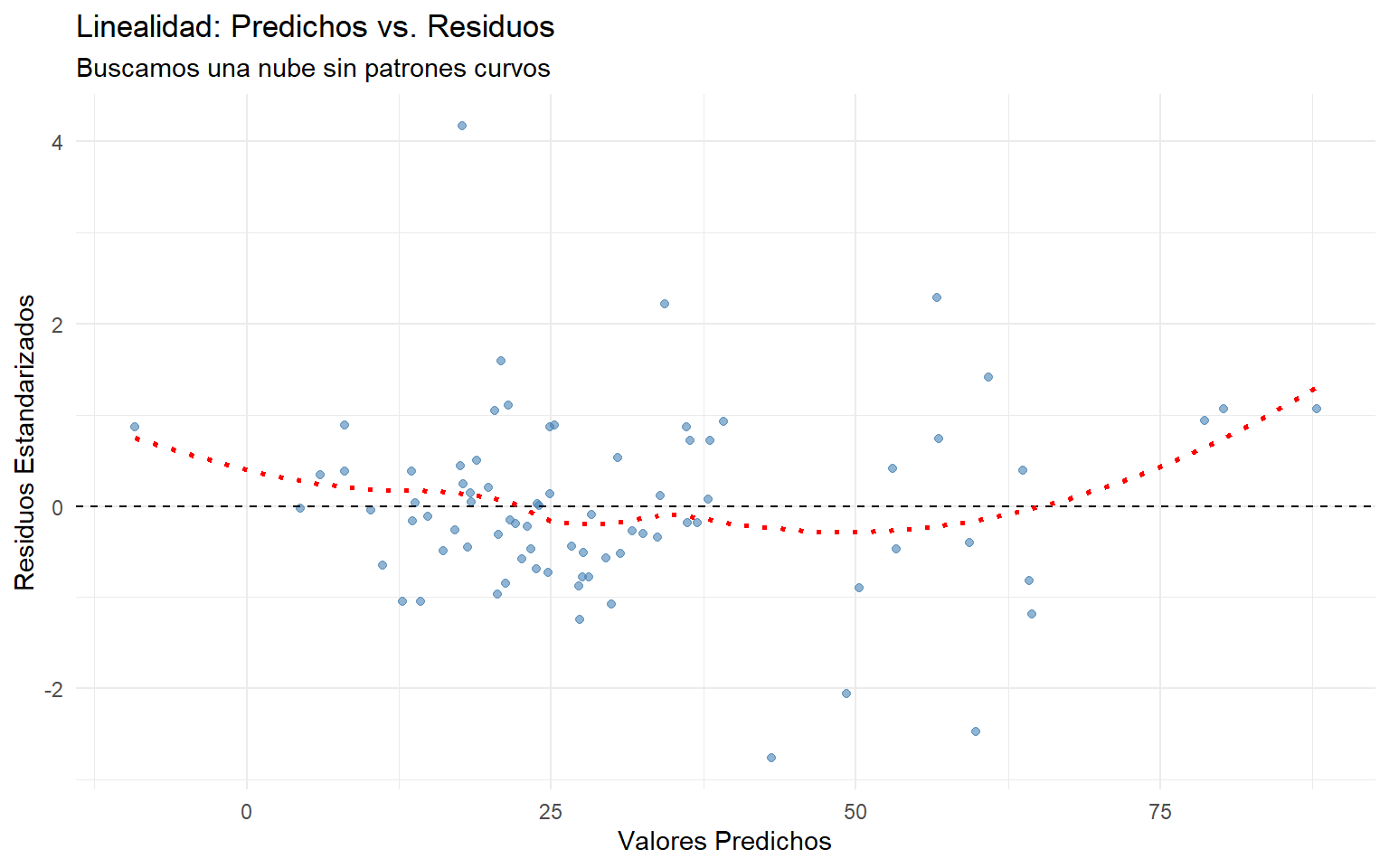
7.5.3 4.3. Supuesto de normalidad de los residuos
Los errores deben distribuirse como una campana de Gauss. Usamos el histograma y el gráfico Q-Q (“las hormigas en el alambre”).
# Histograma
p1 <- ggplot(df_diag, aes(x = residuos_std)) +
geom_histogram(aes(y = ..density..), bins = 15, fill = "steelblue", color = "white", alpha = 0.7) +
geom_density(color = "darkblue", size = 1) +
labs(title = "Histograma de residuos", subtitle = "¿Tiene forma de campana?", x = "Residuos", y = "Densidad") +
theme_minimal()
# Q-Q Plot
p2 <- ggplot(df_diag, aes(sample = residuos_std)) +
stat_qq(color = "steelblue", alpha = 0.6) +
stat_qq_line(linetype = "dashed") +
labs(title = "Gráfico Q-Q Normal", subtitle = "¿Siguen los puntos la línea?", x = "Teórico", y = "Muestra") +
theme_minimal()
p1 + p2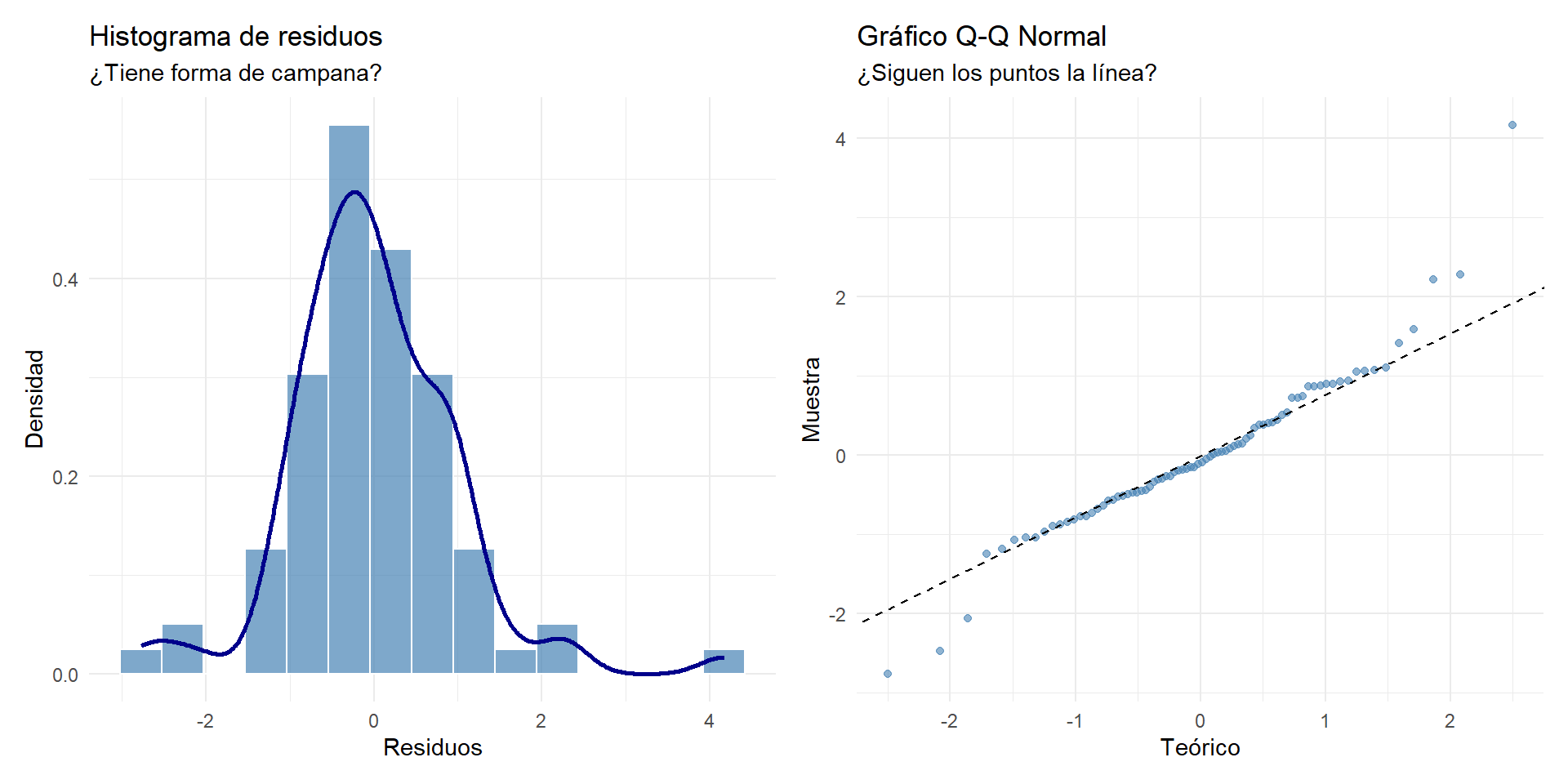
7.5.4 4.4. Supuesto de homocedasticidad
La varianza de los errores debe ser constante. No queremos ver formas de “megáfono” o “embudo”.
# Añadimos variables auxiliares
df_diag <- df_diag %>%
mutate(sqrt_resid = sqrt(abs(residuos_std))) %>%
mutate(tramo = cut_number(predichos, n = 3, labels = c("Bajo", "Medio", "Alto")))
# 1. Dispersión clásica
g1 <- ggplot(df_diag, aes(x = predichos, y = residuos_std)) +
geom_point(color = "steelblue", alpha = 0.6) +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(title = "Dispersión clásica", subtitle = "Buscamos un 'tubo' rectangular", x = "Predichos", y = "Residuos Std.") + theme_minimal()
# 2. Scale-Location
g2 <- ggplot(df_diag, aes(x = predichos, y = sqrt_resid)) +
geom_point(color = "steelblue", alpha = 0.6) +
geom_smooth(method = "loess", color = "darkblue", se = FALSE) +
labs(title = "Scale-Location", subtitle = "La línea roja debe ser horizontal", x = "Predichos", y = "Raíz(|Residuos|)") + theme_minimal()
# 3. Boxplots por tramos
g3 <- ggplot(df_diag, aes(x = tramo, y = residuos_std)) +
geom_boxplot(fill = "steelblue", alpha = 0.4) +
labs(title = "Boxplots por tramos", subtitle = "Las cajas deben tener altura similar", x = "Nivel de Predicción", y = "Residuos Std.") + theme_minimal()
(g1 | g2) / g3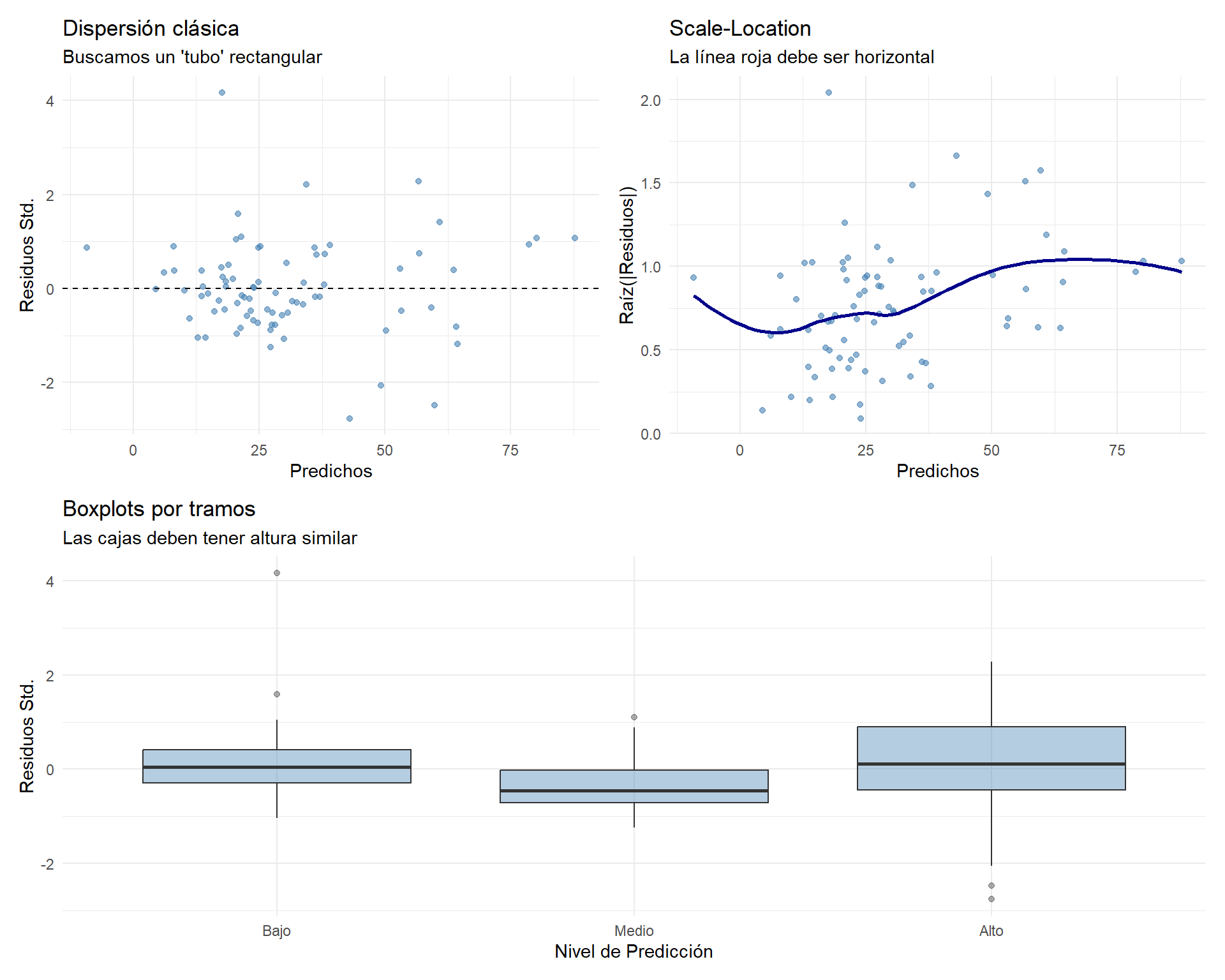
7.5.5 4.5. Supuesto de independencia (Autocorrelación)
Verificamos que los errores no tengan “memoria” (importante si los datos tuvieran orden temporal).
# Test de Durbin-Watson
# Valor ideal: cerca de 2 (entre 1.5 y 2.5 es aceptable)
durbinWatsonTest(modelo1) lag Autocorrelation D-W Statistic p-value
1 0.05652199 1.661074 0.15
Alternative hypothesis: rho != 07.5.6 4.6. Supuesto de no multicolinealidad
Verificamos que las variables independientes no estén demasiado correlacionadas entre sí (que no “canten la misma nota”).
# Factor de Inflación de la Varianza (VIF)
# Regla: VIF > 10 es grave. VIF > 5 es preocupante. Idealmente < 3.
vif(modelo1)asistencia rentabaja extranjero tamclase
1.766354 1.443132 1.019280 1.611180 7.6 5. Validación cruzada (Cross-Validation)
Finalmente, nos preguntamos: ¿Funcionará este modelo en el mundo real con datos nuevos? Para evitar el sobreajuste (overfitting), dividimos la muestra en Entrenamiento (para estudiar) y Prueba (para el examen).
set.seed(123) # Para reproducibilidad
# 1. Dividir la muestra (70% Train / 30% Test)
index <- sample(1:nrow(data), 0.7 * nrow(data))
train_data <- data[index, ]
test_data <- data[-index, ]
# 2. Entrenar el modelo (Solo con el 70%)
modelo_train <- lm(selectivo ~ asistencia + rentabaja + extranjero + tamclase, data = train_data)
r2_train <- summary(modelo_train)$r.squared
# 3. Validar con el examen (Solo con el 30%)
# Predecimos los valores para los datos de prueba
predicciones_test <- predict(modelo_train, newdata = test_data)
# Calculamos el R2 de prueba (Correlación al cuadrado entre Realidad y Predicción)
correlacion_test <- cor(test_data$selectivo, predicciones_test, use='complete.obs')
r2_test <- correlacion_test^2
# 4. Comparación
cat("--- RESULTADOS DE LA VALIDACIÓN ---\n")--- RESULTADOS DE LA VALIDACIÓN ---cat("R² en Entrenamiento (Lo que el modelo aprendió): ", round(r2_train, 4), "\n")R² en Entrenamiento (Lo que el modelo aprendió): 0.801 cat("R² en Prueba (Cómo rinde en el mundo real): ", round(r2_test, 4), "\n")R² en Prueba (Cómo rinde en el mundo real): 0.4706 # Diagnóstico
diferencia <- r2_train - r2_test
if(diferencia > 0.15) {
cat("ALERTA: Hay indicios de sobreajuste (R² cae mucho en prueba).")
} else {
cat("CONCLUSIÓN: El modelo es robusto y generalizable.")
}ALERTA: Hay indicios de sobreajuste (R² cae mucho en prueba).7.7 Conclusiones
Hemos recorrido el proceso completo de un análisis de regresión profesional:
- Exploración: Confirmamos relaciones lineales fuertes.
- Modelización: Construimos un modelo significativo.
- Diagnóstico: Verificamos los supuestos de los residuos (normalidad, homocedasticidad, etc.) para asegurar la validez técnica.
- Validación: Comprobamos mediante Cross-Validation que nuestro modelo no solo memoriza datos, sino que es capaz de predecir en nuevos escenarios.
Este flujo de trabajo asegura que nuestras conclusiones de negocio (qué factores influyen en el rendimiento escolar) estén basadas en una evidencia estadística sólida.