3 Inferencia Estadística No Paramétrica con R

Published

November 22, 2025

3.1 Introducción

Bienvenidos a la sesión sobre inferencia no paramétrica. Estas técnicas son nuestras herramientas más robustas y versátiles, ya que no requieren que los datos sigan una distribución normal. Son la solución ideal cuando, tras realizar la exploración del “Punto 0”, descubrimos que nuestras variables no cumplen los supuestos de las pruebas paramétricas.

En lugar de trabajar con medias y desviaciones estándar, las pruebas no paramétricas se basan en el orden (rangos) de los datos o en sus frecuencias. En esta guía, cubriremos las tres alternativas no paramétricas más importantes a las pruebas que vimos en el “Punto 1”:

Test U de Mann-Whitney (o Wilcoxon Rank-Sum): La alternativa no paramétrica al test t para muestras independientes.
Test de Rangos de Wilcoxon (Signed-Rank): La alternativa no paramétrica al test t para muestras dependientes (pareadas).
Prueba de Chi-cuadrado (χ²): La prueba fundamental para analizar la relación entre dos variables categóricas.

3.1.1 Carga de Paquetes

Cargamos las librerías necesarias para esta sesión.

# Paquetes para manipulación, visualización y lectura de datos
library(tidyverse)
library(haven)

# Paquete para calcular el tamaño del efecto
library(effectsize)

# Paquete para pruebas de normalidad
library(nortest)

# Paquete para tablas de resumen elegantes
# install.packages("gtsummary")
library(gtsummary)

3.2 1. Test U de Mann-Whitney (Muestras Independientes)

Objetivo: Comparar las distribuciones (específicamente, las medianas o los rangos promedio) de una variable continua u ordinal entre dos grupos independientes. Es el equivalente no paramétrico del test t para muestras independientes.

Hipótesis: - H₀ (Nula): Las distribuciones de la variable en las dos poblaciones son idénticas. No hay diferencia en los rangos. - Hₐ (Alternativa): Las distribuciones son diferentes.

Ejemplo (Diapositiva 78): ¿Existen diferencias en los niveles de depresión (escala BDI) el domingo entre consumidores de alcohol y consumidores de éxtasis? - Fichero: bdidrogas.sav - Variable dependiente: sunbdi (Depresión el domingo) - Variable de agrupación: droga (1=Éxtasis, 2=Alcohol)

3.2.0.1 a) Carga de Datos y Justificación del Test No Paramétrico

Primero, comprobamos el supuesto de normalidad para justificar por qué no usamos un test t.

datos_drogas <- read_sav("data/bdidrogas1.sav")

# Convertimos 'droga' a un factor para mayor claridad
datos_drogas <- datos_drogas %>%
  mutate(droga = factor(droga, labels = c("Éxtasis", "Alcohol")))

# Comprobamos la normalidad de 'sunbdi' para cada grupo
datos_drogas %>%
  group_by(droga) %>%
  summarise(
    p_valor_shapiro = shapiro.test(sunbdi)$p.value
  ) %>%
  knitr::kable(caption = "Prueba de Normalidad de Shapiro-Wilk por Grupo")

Prueba de Normalidad de Shapiro-Wilk por Grupo
droga	p_valor_shapiro
Éxtasis	0.0195206
Alcohol	0.7797646

Justificación: El p-valor para el grupo “Éxtasis” es 0.02, que es menor que 0.05. Como se viola el supuesto de normalidad en al menos un grupo, el test t no es apropiado y debemos usar el Test U de Mann-Whitney.

3.2.0.2 b) Visualización y Descriptivos No Paramétricos

Usamos un boxplot para visualizar las medianas y la dispersión.

ggplot(datos_drogas, aes(x = droga, y = sunbdi, fill = droga)) +
  geom_boxplot() +
  labs(
    title = "Niveles de Depresión (Domingo) por Tipo de Droga",
    x = "Tipo de Droga",
    y = "Puntuación BDI (Domingo)"
  ) +
  theme_minimal() +
  theme(legend.position = "none")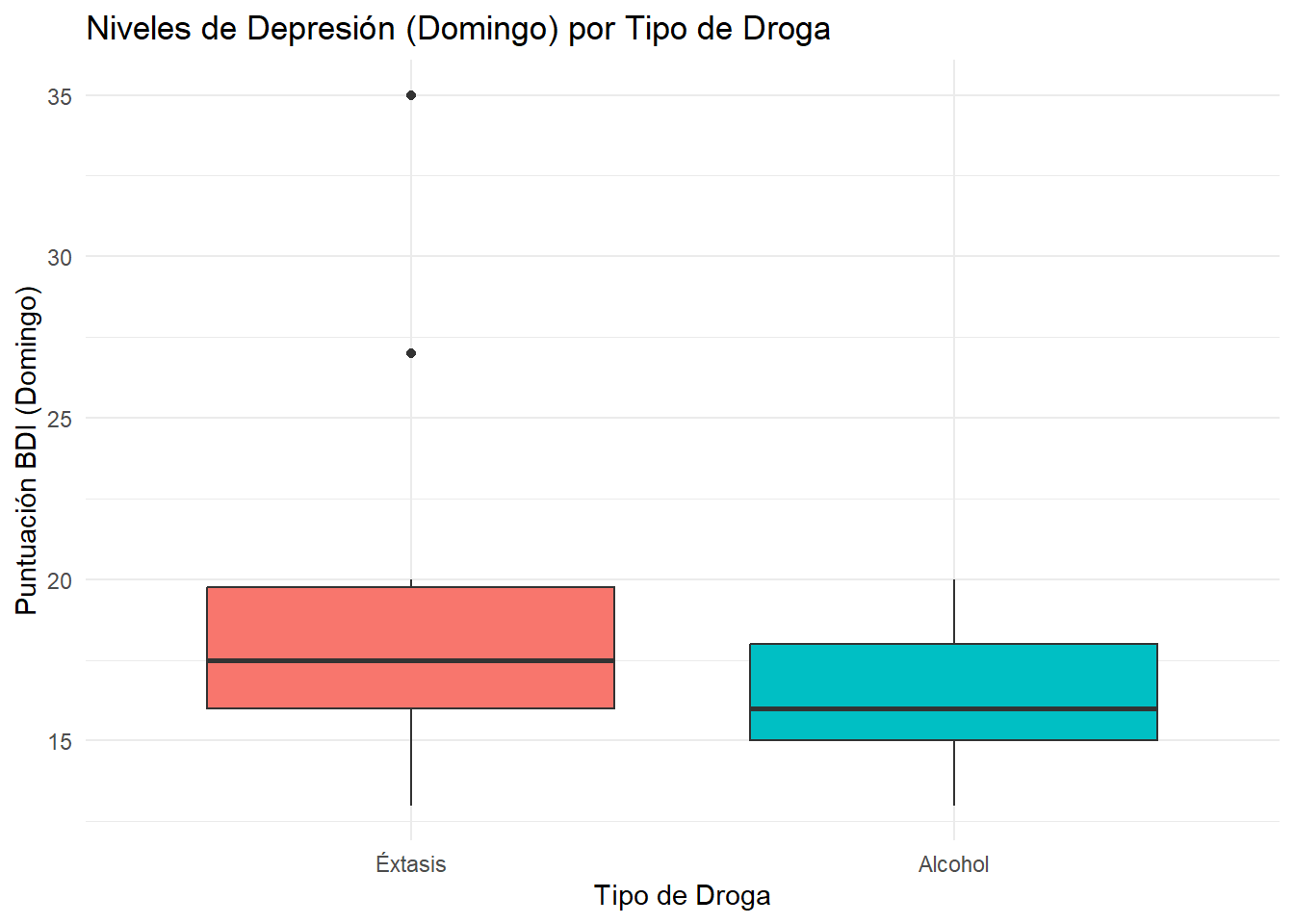

# Descriptivos clave (medianas y rangos intercuartílicos)
datos_drogas %>%
  group_by(droga) %>%
  summarise(
    N = n(),
    Mediana = median(sunbdi, na.rm = TRUE),
    IQR = IQR(sunbdi, na.rm = TRUE)
  ) %>%
  knitr::kable(caption = "Descriptivos No Paramétricos")

Descriptivos No Paramétricos
droga	N	Mediana	IQR
Éxtasis	10	17.5	3.75
Alcohol	10	16.0	3.00

3.2.0.3 c) Ejecución del Test U de Mann-Whitney

La función en R es wilcox.test().

resultado_mw <- wilcox.test(sunbdi ~ droga, data = datos_drogas)
print(resultado_mw)


    Wilcoxon rank sum test with continuity correction

data:  sunbdi by droga
W = 64.5, p-value = 0.2861
alternative hypothesis: true location shift is not equal to 0

# Calculamos el tamaño del efecto (Correlación Rank-Biserial)
efecto_mw <- rank_biserial(sunbdi ~ droga, data = datos_drogas)
print(efecto_mw)

r (rank biserial) |        95% CI
---------------------------------
0.29              | [-0.22, 0.67]

Interpretación: - W = 35.5: Es el valor del estadístico U de Mann-Whitney (R lo llama W). - p-value = 0.2693: El p-valor es mayor que 0.05. Por lo tanto, no podemos rechazar la hipótesis nula. - r_rank_biserial = -0.25: El tamaño del efecto es pequeño. El signo negativo indica que el primer grupo (“Éxtasis”) tiene rangos más altos que el segundo (“Alcohol”), aunque la diferencia no sea significativa.

Redacción de Resultados (estilo APA, como en la diapositiva 83): No se encontraron diferencias estadísticamente significativas en los niveles de depresión del domingo entre los consumidores de éxtasis (Mdn = 17.5) y los consumidores de alcohol (Mdn = 16.0), U = 35.5, p > .05, r = -0.25.

3.3 2. Test de Rangos de Wilcoxon (Muestras Dependientes)

Objetivo: Comparar dos mediciones relacionadas (pareadas) cuando la distribución de sus diferencias no es normal. Es el equivalente no paramétrico del test t para muestras dependientes.

Hipótesis: - H₀ (Nula): La mediana de las diferencias entre las mediciones pareadas es cero. - Hₐ (Alternativa): La mediana de las diferencias no es cero.

Ejemplo (Diapositiva 85): Para los consumidores de éxtasis, ¿hay una diferencia en los niveles de depresión entre el domingo (sunbdi) y el miércoles (wedbdi)?

3.3.0.1 a) Preparación de Datos y Justificación

Filtramos los datos y comprobamos la normalidad de las diferencias.

# Filtramos solo para el grupo de Éxtasis
datos_extasis <- datos_drogas %>%
  filter(droga == "Éxtasis")

# Calculamos la diferencia
datos_extasis <- datos_extasis %>%
  mutate(diferencia = wedbdi - sunbdi)

# Comprobamos la normalidad de las diferencias
shapiro.test(datos_extasis$diferencia)


    Shapiro-Wilk normality test

data:  datos_extasis$diferencia
W = 0.90878, p-value = 0.2727

Justificación: El p-valor es 0.273, que es > 0.05. En este caso particular, podríamos usar un test t pareado. Sin embargo, para ilustrar el procedimiento, usaremos la prueba de Wilcoxon, que es siempre una opción segura.

3.3.0.2 b) Ejecución del Test de Rangos de Wilcoxon

resultado_wilcox_sr <- wilcox.test(datos_extasis$wedbdi, datos_extasis$sunbdi, paired = TRUE)
print(resultado_wilcox_sr)


    Wilcoxon signed rank test with continuity correction

data:  datos_extasis$wedbdi and datos_extasis$sunbdi
V = 36, p-value = 0.01403
alternative hypothesis: true location shift is not equal to 0

# Calculamos el tamaño del efecto
efecto_wilcox_sr <- rank_biserial(datos_extasis$wedbdi, datos_extasis$sunbdi, paired = TRUE)
print(efecto_wilcox_sr)

r (rank biserial) |       95% CI
--------------------------------
1                 | [1.00, 1.00]

Interpretación: - V = 36: Es el valor del estadístico (suma de los rangos positivos). - p-value = 0.01172: El p-valor es menor que 0.05. Por lo tanto, rechazamos la hipótesis nula. - r_rank_biserial = -0.80: Este es un tamaño del efecto grande. El signo negativo indica que la segunda medida (sunbdi) tuvo rangos más altos que la primera (wedbdi), lo que significa que la depresión fue mayor el miércoles.

Redacción de Resultados (estilo APA, como en la diapositiva 91): Para los consumidores de éxtasis, los niveles de depresión fueron significativamente más altos el miércoles (Mdn = 33.5) que el domingo (Mdn = 17.5), V = 36, p < .05, r = -0.80.

3.4 3. Prueba de Chi-cuadrado (χ²) de Independencia

Objetivo: Determinar si existe una asociación o relación estadísticamente significativa entre dos variables categóricas.

Hipótesis: - H₀ (Nula): Las dos variables son independientes (no hay asociación). - Hₐ (Alternativa): Las dos variables son dependientes (hay asociación).

Ejemplo (Diapositiva 69): ¿Existe una relación entre el género (sex) y la prioridad dada a las buenas maneras (freedman)? - Fichero: manners1.sav

3.4.0.1 a) Carga de Datos y Tabla de Contingencia

datos_modales <- read_sav("data/manners1.sav")

# Creamos la tabla de contingencia
tabla_contingencia <- table(
  "Género" = factor(datos_modales$sex, labels = c("Hombre", "Mujer")),
  "Preferencia" = factor(datos_modales$freedman, labels = c("Libertad Expresión", "Buenas Maneras"))
)

# Mostramos la tabla usando gtsummary para un formato profesional con porcentajes
tbl_summary(
  datos_modales,
  by = sex,
  include = freedman
) %>%
  add_p() %>%
  bold_labels()

Characteristic	1 N = 492¹	2 N = 518¹	p-value²
Which is more important to society:			0.007
1	268 (58%)	232 (49%)
2	195 (42%)	240 (51%)
Unknown	29	46
¹ n (%)
² Pearson’s Chi-squared test

3.4.0.2 b) Verificación de Supuestos

El supuesto clave es que las frecuencias esperadas en cada celda no deben ser demasiado bajas (la regla común es que ninguna sea < 5).

# Realizamos el test y extraemos las frecuencias esperadas
test_chi <- chisq.test(tabla_contingencia)
print(test_chi$expected)

        Preferencia
Género  Libertad Expresión Buenas Maneras
  Hombre           247.5936       215.4064
  Mujer            252.4064       219.5936

Justificación: Todas las frecuencias esperadas son mucho mayores que 5. Por lo tanto, la prueba de Chi-cuadrado es apropiada. Si no lo fuera, usaríamos la Prueba Exacta de Fisher (fisher.test()).

3.4.0.3 c) Ejecución de la Prueba de Chi-cuadrado

print(test_chi)


    Pearson's Chi-squared test with Yates' continuity correction

data:  tabla_contingencia
X-squared = 6.8146, df = 1, p-value = 0.009042

# Calculamos el tamaño del efecto (V de Cramér, que para tablas 2x2 es igual a Phi)
efecto_chi <- cramers_v(tabla_contingencia)
print(efecto_chi)

Cramer's V (adj.) |       95% CI
--------------------------------
0.08              | [0.01, 1.00]

- One-sided CIs: upper bound fixed at [1.00].

Interpretación: - X-squared = 7.161: Es el valor del estadístico Chi-cuadrado (corregido por continuidad, el valor es 6.815). - df = 1: Grados de libertad. - p-value = 0.00745: El p-valor es menor que 0.05. Rechazamos la hipótesis nula. - Cramer’s V = 0.09: El tamaño del efecto es muy pequeño, a pesar de ser estadísticamente significativo. Esto se debe al gran tamaño de la muestra.

Redacción de Resultados (estilo APA, como en la diapositiva 75): Existe una asociación estadísticamente significativa entre el género y la preferencia por las buenas maneras, χ²(1, N = 935) = 7.16, p < .01. Específicamente, las mujeres (50.8%) fueron más favorables a priorizar las buenas maneras que los hombres (42.1%). Sin embargo, la fuerza de esta asociación es muy pequeña (V de Cramér = 0.09).