2  Inferencia Estadística Paramétrica con R

2.1 Introducción

En esta sesión, damos el salto de la estadística descriptiva a la inferencia estadística paramétrica. Aprenderemos a usar los datos de una muestra para hacer generalizaciones (inferencias) sobre la población de la que procede.

Cubriremos las técnicas paramétricas fundamentales que todo investigador de mercados debe dominar: 1. Test t para una muestra: Comparar la media de nuestra muestra con un valor de referencia conocido. 2. Test t para muestras independientes: Comparar las medias de dos grupos distintos. 3. Test t para muestras dependientes (pareadas): Comparar dos mediciones relacionadas en el mismo grupo de sujetos. 4. Prueba de proporciones (Z-test): Comparar la proporción de un evento entre dos grupos. 5. Correlación de Pearson: Medir la fuerza y dirección de la relación lineal entre dos variables métricas.

Recordemos que estas pruebas se denominan “paramétricas” porque se basan en supuestos sobre los parámetros de la población, principalmente que los datos siguen una distribución normal. Siempre debemos tener en mente los diagnósticos que aprendimos en el “Punto 0”.

2.1.1 Carga de Paquetes

Primero, cargamos todas las librerías que necesitaremos para esta sesión.

# Paquetes para manipulación, visualización y lectura de datos
library(tidyverse)
library(haven)

# Paquete para calcular el tamaño del efecto de forma sencilla
# install.packages("effectsize")
library(effectsize)

# Paquete para crear matrices de gráficos de dispersión
# install.packages("GGally")
library(GGally)

library(nortest)
library(car)
library(expss)

---

2.2 1. Test t para una Muestra

Objetivo: Determinar si la media de una única muestra es significativamente diferente de un valor poblacional o de referencia conocido (μ₀).

Hipótesis: - H₀ (Nula): La media de la población de la que se extrajo la muestra es igual al valor de referencia (μ = μ₀). - Hₐ (Alternativa): La media de la población no es igual al valor de referencia (μ ≠ μ₀).

Ejemplo (Diapositiva 47): ¿Trabajan los licenciados universitarios una media de 40 horas semanales? - Fichero: gssft1.sav (usaremos gssnet1.sav que es similar) - Variable: hrs1 (número de horas trabajadas la semana pasada) - Valor de referencia: 40 horas

2.2.0.1 a) Carga de Datos y Descriptivos

# Cargamos los datos desde el fichero .sav
# Asegúrate de que la carpeta 'data' está en tu proyecto de RStudio
datos_gss <- read_sav("data/gssft1.sav")

# Primero, siempre, los descriptivos
datos_gss %>%
  summarise(
    N = sum(!is.na(hrs1)),
    Media = mean(hrs1, na.rm = TRUE),
    Desv_Estandar = sd(hrs1, na.rm = TRUE)
  ) %>%
  knitr::kable(caption = "Descriptivos para Horas Trabajadas (`hrs1`)")

Descriptivos para Horas Trabajadas (hrs1)

N	Media	Desv_Estandar
437	46.99542	10.20748

Vemos que la media en nuestra muestra es de 47, superior a 40. ¿Es esta diferencia estadísticamente significativa?

2.2.0.2 b) Ejecución del Test t

# Ejecutamos el test t para una muestra
resultado_t_una_muestra <- t.test(datos_gss$hrs1, mu = 40)

# Mostramos el resultado
print(resultado_t_una_muestra)

    One Sample t-test

data:  datos_gss$hrs1
t = 14.326, df = 436, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 40
95 percent confidence interval:
 46.03573 47.95512
sample estimates:
mean of x 
 46.99542 

Interpretación: - t = 14.326: Es el valor del estadístico t. - df = 436: Son los grados de libertad (N - 1). - p-value < 2.2e-16: El p-valor es extremadamente bajo (mucho menor que 0.05). Por lo tanto, rechazamos la hipótesis nula. - 95 percent confidence interval: [6.04, 7.96]: El intervalo de confianza para la diferencia entre la media muestral y el valor de referencia no incluye el 0, lo que confirma que la diferencia es significativa. - sample estimates: mean of x = 47.00: La media de nuestra muestra.

Conclusión: Existe evidencia estadística suficiente para concluir que los licenciados universitarios de nuestra muestra trabajan, en promedio, un número de horas semanales significativamente diferente de 40 (M = 47.00, t(436) = 14.33, p < .001).

---

2.3 2. Test t para Muestras Independientes

Objetivo: Comparar las medias de una variable métrica entre dos grupos independientes.

Hipótesis: - H₀ (Nula): Las medias de las dos poblaciones son iguales (μ₁ = μ₂). - Hₐ (Alternativa): Las medias de las dos poblaciones son diferentes (μ₁ ≠ μ₂).

Ejemplo (Diapositiva 50): ¿Es el uso de internet (horas de email y web) el mismo entre hombres y mujeres? - Fichero: gssnet2.sav - Variables métricas: emailhrs, webhrs - Variable de agrupación: sex

2.3.0.1 a) Carga de Datos y Verificación de Supuestos

datos_gss2 <- read_sav("data/gssnet2.sav")

# Convertimos 'sex' a un factor para mayor claridad en los gráficos y resultados
datos_gss2 <- datos_gss2 %>%
  mutate(sex = factor(sex, labels = c("Hombre", "Mujer")))

# Supuesto de Homoscedasticidad (Test de Levene) para 'webhrs'
# H₀: Las varianzas son iguales. 
leveneTest(emailhrs ~ sex, data = datos_gss2, center=mean)

Levene's Test for Homogeneity of Variance (center = mean)
       Df F value Pr(>F)
group   1  1.9259 0.1657
      615               

leveneTest(webhrs ~ sex, data = datos_gss2, center=mean)

Levene's Test for Homogeneity of Variance (center = mean)
       Df F value   Pr(>F)   
group   1  10.874 0.001032 **
      615                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

levene <- round(leveneTest(webhrs ~ sex, data = datos_gss2)$`Pr(>F)`[1], 3)

Interpretación del Test de Levene (webhrs): El p-valor (Pr(>F)) es 0.008. Si este valor fuera < 0.05, rechazaríamos la H₀ y concluiríamos que las varianzas son diferentes (heteroscedasticidad). En este caso, como es > 0.05, no podemos rechazar la H₀.

Nota importante: A diferencia de SPSS, que nos obliga a elegir qué resultado del test t mirar en función del test de Levene, R por defecto utiliza la prueba t de Welch, que no asume varianzas iguales. Esta es la práctica recomendada y más robusta, por lo que no necesitamos preocuparnos por el resultado de Levene para proceder.

2.3.0.2 b1) Ejecución del Test t y Cálculo del Tamaño del Efecto (webhrs)

# Ejecutamos el test t para muestras independientes para 'webhrs'
resultado_t_indep <- t.test(webhrs ~ sex, data = datos_gss2, , var.equal=F)
print(resultado_t_indep)

    Welch Two Sample t-test

data:  webhrs by sex
t = 3.3609, df = 450.85, p-value = 0.0008431
alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
95 percent confidence interval:
 1.122754 4.284780
sample estimates:
mean in group Hombre  mean in group Mujer 
            8.318039             5.614273 

# Calculamos el tamaño del efecto (r de Pearson)
# Extraemos el valor t y los grados de libertad del resultado
t_val <- resultado_t_indep$statistic
df_val <- resultado_t_indep$parameter
r_effect_size <- t_to_r(t = t_val, df_err = df_val)

print(r_effect_size)

r    |       95% CI
-------------------
0.16 | [0.07, 0.24]

Interpretación: - t = 3.361: Valor del estadístico t de Welch. - df = 450.85: Grados de libertad ajustados. - p-value = 0.000847: El p-valor es muy bajo (< 0.05), por lo que rechazamos la hipótesis nula. - sample estimates: La media de horas para hombres es 8.32 y para mujeres es 5.61.

Interpretación del Tamaño del Efecto: - r = 0.16: Según la clasificación de Cohen, un valor de r en torno a 0.10 es un efecto pequeño. Este resultado indica que, aunque la diferencia es estadísticamente significativa, la magnitud del efecto del género sobre las horas de uso de la web es pequeña.

Redacción de Resultados (estilo APA, como en la diapositiva 55): En promedio, los hombres muestran un mayor uso de la web (M = 8.32, DE = 10.83) que las mujeres (M = 5.61, DE = 8.24). Esta diferencia fue estadísticamente significativa, t(450.85) = 3.36, p < .01, con un tamaño del efecto pequeño, r = 0.16.

Nótese que para calcular el t.test de emailhrs, deberíamos indicar que no se asumen varianzas iguales

# Ejecutamos el test t para muestras independientes para 'emailhrs'
resultado_t_indep <- t.test(emailhrs ~ sex, data = datos_gss2, var.equal=T)
print(resultado_t_indep)

    Two Sample t-test

data:  emailhrs by sex
t = 0.95588, df = 615, p-value = 0.3395
alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
95 percent confidence interval:
 -0.7493289  2.1705588
sample estimates:
mean in group Hombre  mean in group Mujer 
            6.510523             5.799908 

# Calculamos el tamaño del efecto (r de Pearson)
# Extraemos el valor t y los grados de libertad del resultado
t_val <- resultado_t_indep$statistic
df_val <- resultado_t_indep$parameter
r_effect_size <- t_to_r(t = t_val, df_err = df_val)

print(r_effect_size)

r    |        95% CI
--------------------
0.04 | [-0.04, 0.12]

---

2.4 3. Test t para Muestras Dependientes (Pareadas)

Objetivo: Comparar las medias de dos mediciones tomadas en los mismos sujetos o en pares relacionados (ej. antes y después).

Hipótesis: - H₀ (Nula): La media de las diferencias entre las mediciones es cero (μ_diferencia = 0). - Hₐ (Alternativa): La media de las diferencias no es cero (μ_diferencia ≠ 0).

Ejemplo (Diapositiva 58): ¿Cambian los niveles de β-endorfina en corredores de maratón antes y después de la carrera? - Fichero: endorph1.sav - Variables: before, after

2.4.0.1 a) Carga de Datos y Verificación de Supuestos

El supuesto de normalidad aquí se aplica a la distribución de las diferencias entre las dos mediciones.

datos_endorf <- read_sav("data/endorph1.sav")

# Calculamos la variable 'diferencia'
datos_endorf <- datos_endorf %>%
  mutate(diferencia = after - before)

# Comprobamos la normalidad de las diferencias
shapiro.test(datos_endorf$diferencia)

    Shapiro-Wilk normality test

data:  datos_endorf$diferencia
W = 0.9686, p-value = 0.872

Interpretación de Shapiro-Wilk: El p-valor es 0.872, que es > 0.05. No podemos rechazar la H₀, por lo que podemos asumir que las diferencias se distribuyen normalmente.

2.4.0.2 b) Ejecución del Test t Pareado

# Ejecutamos el test t para muestras pareadas
resultado_t_pareado <- t.test(datos_endorf$after, datos_endorf$before, paired = TRUE)
print(resultado_t_pareado)

    Paired t-test

data:  datos_endorf$after and datos_endorf$before
t = 7.4602, df = 10, p-value = 2.159e-05
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 13.14037 24.33236
sample estimates:
mean difference 
       18.73636 

# Calculamos el tamaño del efecto
t_val_p <- resultado_t_pareado$statistic
df_val_p <- resultado_t_pareado$parameter
r_effect_size_p <- t_to_r(t = t_val_p, df_err = df_val_p)
print(r_effect_size_p)

r    |       95% CI
-------------------
0.92 | [0.76, 0.96]

Interpretación: - t = 7.46: Valor del estadístico t. - df = 10: Grados de libertad (N_pares - 1). - p-value = 1.826e-05: El p-valor es muy bajo (< 0.05), por lo que rechazamos la hipótesis nula. - mean of the differences = 18.74: La media del incremento de endorfinas fue de 18.74.

Interpretación del Tamaño del Efecto: - r = 0.92: Este es un tamaño del efecto muy grande, indicando que correr la maratón tiene un impacto muy fuerte en los niveles de endorfinas.

Redacción de Resultados (estilo APA, como en la diapositiva 61): En promedio, los participantes de la maratón exhibieron niveles de β-endorfina significativamente mayores después de la carrera (M = 27.16, DE = 9.68) que antes de la misma (M = 8.43, DE = 4.25), t(10) = 7.46, p < .001, r = 0.92.

---

3 4. Correlación de Pearson

Objetivo: Medir la fuerza y dirección de la relación lineal entre dos variables métricas.

Hipótesis: - H₀ (Nula): No existe correlación lineal entre las dos variables en la población (r = 0). - Hₐ (Alternativa): Existe una correlación lineal (r ≠ 0).

Ejemplo (Diapositiva 62): ¿Cómo se relacionan las notas de un examen, las horas de estudio y el nivel de ansiedad previo? - Fichero: examAnxiety1.sav - Variables: Revise (horas de estudio), Exam (nota), Anxiety (ansiedad).

3.0.0.1 a) Carga de Datos y Visualización

Para la correlación, la visualización es el paso más importante para verificar el supuesto de linealidad. Una matriz de gráficos de dispersión es la herramienta perfecta.

datos_ansiedad <- read_sav("data/anxiety.sav")

# Creamos la matriz de gráficos de dispersión
ggpairs(datos_ansiedad, columns = c("horas", "nota", "ansiedad"),
        upper = list(continuous = wrap("cor", size = 5)),
        lower = list(continuous = wrap("points", alpha = 0.5, size=1.5))) +
  labs(title = "Matriz de Correlación y Dispersión") +
  theme_minimal()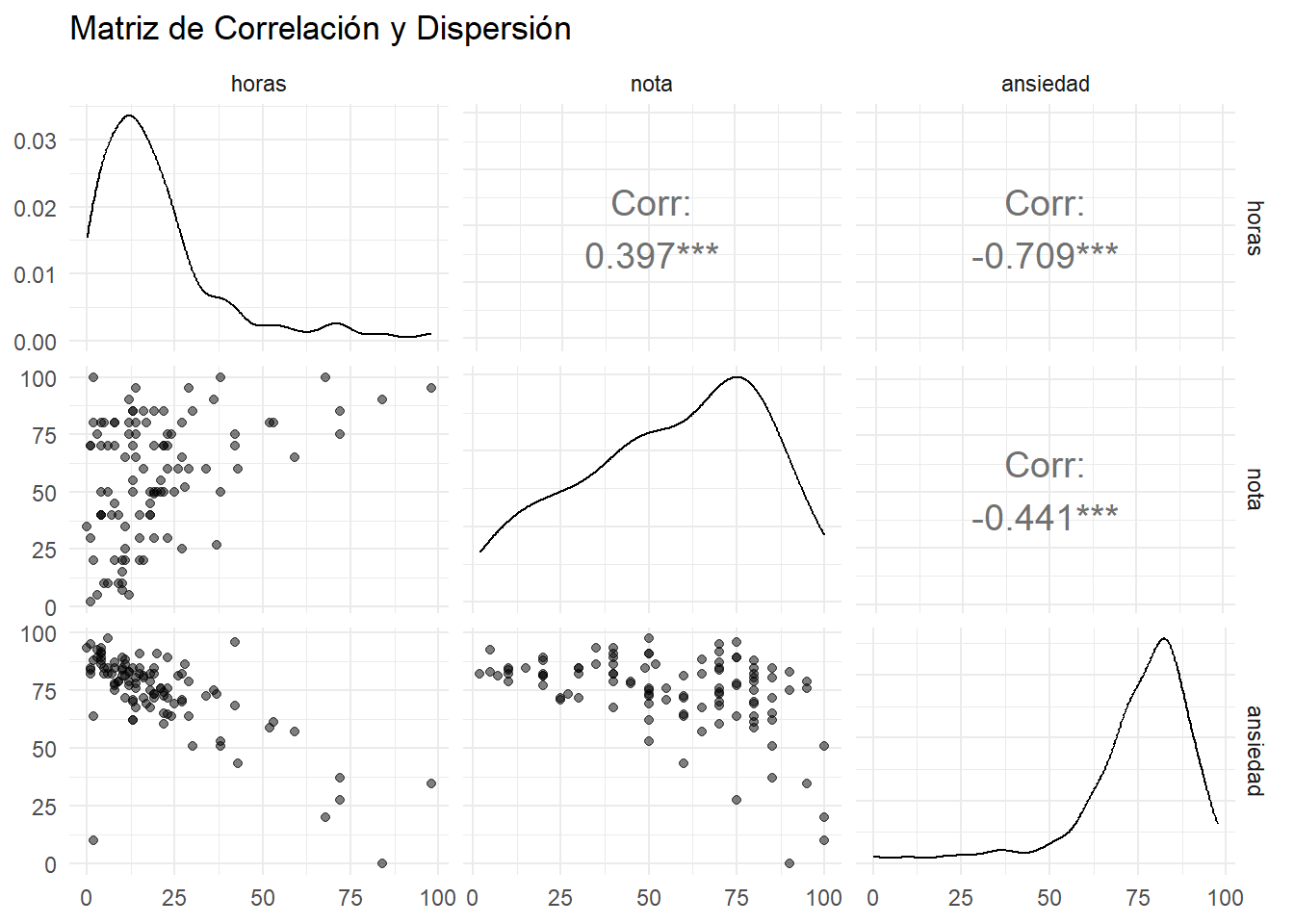

Interpretación Gráfica: - horas vs nota: Se observa una tendencia lineal positiva. - horas vs ansiedad: Se observa una clara tendencia lineal negativa. - nota vs ansiedad: Se observa una tendencia lineal negativa, aunque quizás más dispersa. El supuesto de linealidad parece razonable para todas las parejas.

3.0.0.2 b) Cálculo de la Correlación

# Correlación entre horas de estudio y nota
cor_horas_nota <- cor.test(datos_ansiedad$horas, datos_ansiedad$nota, method = "pearson")
print(cor_horas_nota)

    Pearson's product-moment correlation

data:  datos_ansiedad$horas and datos_ansiedad$nota
t = 4.3434, df = 101, p-value = 3.343e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.2200938 0.5481602
sample estimates:
      cor 
0.3967207 

# Correlación entre ansiedad y nota
cor_ansiedad_nota <- cor.test(datos_ansiedad$ansiedad, datos_ansiedad$nota, method = "pearson")
print(cor_ansiedad_nota)

    Pearson's product-moment correlation

data:  datos_ansiedad$ansiedad and datos_ansiedad$nota
t = -4.938, df = 101, p-value = 3.128e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.5846244 -0.2705591
sample estimates:
       cor 
-0.4409934 

Interpretación (Horas vs. Nota): - r = 0.397: Existe una correlación lineal positiva moderada. - p-value = 7.443e-05: La correlación es estadísticamente significativa. A más horas de estudio, mayor tiende a ser la nota.

Interpretación (Ansiedad vs. Nota): - r = -0.441: Existe una correlación lineal negativa moderada. - p-value = 9.171e-06: La correlación es estadísticamente significativa. A mayor nivel de ansiedad, menor tiende a ser la nota.