# Cargamos las librerías que vamos a necesitar
library(haven)
library(Hmisc)
library(psych)5 Análisis de componentes principales (ACP)
Reduciendo el espacio dimensional con R
5.1 Introducción
Este documento es una guía práctica que replica en R el análisis de componentes principales (ACP) realizado en la sesión de clase con SPSS, utilizando el caso de la empresa HBAT. El objetivo es doble:
- Reducir la dimensionalidad: Partimos de 13 variables que miden la percepción de los clientes sobre HBAT. Buscamos agruparlas en un número menor de “dimensiones” o “componentes” subyacentes que sean más fáciles de interpretar y gestionar.
- Contar una historia de marketing: Queremos que estos nuevos componentes tengan sentido de negocio y nos ayuden a entender mejor las fortalezas y debilidades de HBAT desde la perspectiva del cliente.
5.1.1 Paquetes necesarios
Para este análisis, utilizaremos varios paquetes de R. Es importante tenerlos instalados (install.packages("nombre_paquete")) antes de empezar.
haven: Para leer archivos de datos de SPSS (.sav).Hmisc: Proporciona la funciónrcorr()para calcular matrices de correlación y sus p-valores de forma sencilla.psych: El paquete estrella para este análisis. Contiene las funcionesKMO(),bartlett.test()y, lo más importante,principal()para realizar el ACP.
5.2 1. Carga y preparación de los datos
El primer paso es cargar el conjunto de datos de HBAT y seleccionar únicamente las 13 variables métricas (de x6 a x18) que formarán parte de nuestro análisis.
# Leemos el fichero de datos directamente desde la URL
hbat <- read_spss("data/hbat.sav")
# Creamos un dataframe llamado 'data00' solo con las variables de interés
data00 <- subset(hbat, select = c(x6, x7, x8, x9, x10, x11, x12, x13, x14, x15, x16, x17, x18))
# Echamos un vistazo a las primeras filas para confirmar que todo está correcto
head(data00)# A tibble: 6 × 13
x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 8.5 3.9 2.5 5.9 4.8 4.9 6 6.8 4.7 4.3 5 5.1 3.7
2 8.2 2.7 5.1 7.2 3.4 7.9 3.1 5.3 5.5 4 3.9 4.3 4.9
3 9.2 3.4 5.6 5.6 5.4 7.4 5.8 4.5 6.2 4.6 5.4 4 4.5
4 6.4 3.3 7 3.7 4.7 4.7 4.5 8.8 7 3.6 4.3 4.1 3
5 9 3.4 5.2 4.6 2.2 6 4.5 6.8 6.1 4.5 4.5 3.5 3.5
6 6.5 2.8 3.1 4.1 4 4.3 3.7 8.5 5.1 9.5 3.6 4.7 3.35.3 2. Diagnóstico de adecuación: El “casting” de las variables
Antes de lanzar el análisis, debemos asegurarnos de que nuestras variables son adecuadas. No todas las variables sirven para un ACP. Necesitamos “jugadoras de equipo”, variables que estén suficientemente correlacionadas entre sí para poder formar grupos coherentes. Este proceso es como un “casting” para una película: solo las variables que cumplan los requisitos pasarán a la siguiente fase.
5.3.1 2.1. El “Índice de Colaboración” (KMO y MSA)
La prueba de Kaiser-Meyer-Olkin (KMO) es nuestra principal herramienta de casting. Nos da dos métricas clave:
- KMO general: Un valor global que nos dice si el conjunto de datos en su totalidad es adecuado. Es como el “clima laboral” de la oficina. Un valor > 0.7 es bueno.
- MSA (Measure of Sampling Adequacy): Un valor individual para cada variable. Es el “índice de colaboración” de cada empleado. La regla de oro es que ninguna variable debe tener un MSA inferior a 0.5. Una variable con un MSA bajo es un “lobo solitario”: no se correlaciona bien con el resto y solo añade ruido.
Proceso a seguir: Si encontramos variables con MSA < 0.5, debemos eliminar solo la que tenga el valor más bajo, y volver a ejecutar la prueba. Este proceso se repite hasta que todas las variables cumplan el criterio.
5.3.1.1 Primer intento
KMO(data00)Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = data00)
Overall MSA = 0.61
MSA for each item =
x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18
0.87 0.62 0.53 0.89 0.81 0.45 0.59 0.88 0.53 0.31 0.86 0.44 0.53 Diagnóstico: El KMO general es de 0.65 (“mediocre” pero aceptable para empezar). Sin embargo, al mirar los MSA individuales, vemos varios problemas. La variable x15 tiene un MSA de 0.31, muy por debajo del umbral. Es nuestro primer “lobo solitario” y debe ser eliminada.
5.3.1.2 Segundo intento (sin X15)
# Creamos un nuevo dataframe sin la variable x15
data01 <- subset(data00, select = -c(x15))
# Volvemos a calcular el KMO
KMO(data01)Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = data01)
Overall MSA = 0.61
MSA for each item =
x6 x7 x8 x9 x10 x11 x12 x13 x14 x16 x17 x18
0.88 0.62 0.53 0.89 0.80 0.45 0.59 0.88 0.53 0.86 0.44 0.53 Diagnóstico: El KMO general ha mejorado a 0.68. ¡Buena señal! Sin embargo, ahora x17 es la variable con el MSA más bajo (0.44). Aún no cumplimos los requisitos, así que la eliminamos.
5.3.1.3 Tercer intento (sin X15 ni X17)
# Creamos un nuevo dataframe sin x15 y x17
data02 <- subset(data01, select = -c(x17))
# Calculamos el KMO por última vez en esta fase
KMO(data02)Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = data02)
Overall MSA = 0.65
MSA for each item =
x6 x7 x8 x9 x10 x11 x12 x13 x14 x16 x18
0.51 0.63 0.52 0.79 0.78 0.62 0.62 0.75 0.51 0.76 0.67 Diagnóstico: ¡Perfecto! El KMO general ha subido a 0.71 (“medio” o bueno) y, lo más importante, todas las variables tienen un MSA individual por encima de 0.5. Notemos cómo x11, que antes estaba en duda con un MSA de 0.45, ahora es aceptable con 0.53. Esto demuestra la importancia de este proceso iterativo. Nuestro “casting” ha terminado y tenemos nuestro conjunto final de variables para el análisis.
5.3.2 2.2. Test de Esfericidad de Bartlett
Este test es un control de seguridad final. Responde a la pregunta: ¿existe suficiente correlación en nuestros datos como para que valga la pena buscar una estructura?
- Hipótesis Nula (Ho): La matriz de correlaciones es una matriz identidad (no hay correlación entre las variables).
- Nuestro objetivo: Queremos un resultado significativo (p-valor < 0.05) para poder rechazar la Ho. Un p-valor bajo es una buena noticia, significa que hay material para analizar.
# El test de Bartlett se aplica sobre el dataframe final validado
cortest.bartlett(data02)$chisq
[1] 619.2726
$p.value
[1] 1.79337e-96
$df
[1] 55Diagnóstico: El p-valor es prácticamente cero (p-value = 0). Por lo tanto, rechazamos con contundencia la hipótesis nula. Hay correlaciones significativas en nuestros datos y tenemos “luz verde” para proceder con el ACP.
5.4 3. Extracción e interpretación de componentes
Con nuestro set de datos validado (data02), es hora de realizar el análisis. El primer paso crucial es decidir cuántos componentes vamos a retener. No queremos ni demasiados (perdemos el objetivo de reducir datos) ni demasiado pocos (perdemos información valiosa).
5.4.1 3.1. ¿Cuántos componentes retener? El criterio del autovalor
La regla más común y objetiva es el Criterio de Kaiser: retener solo aquellos componentes cuyo autovalor (Eigenvalue) sea mayor que 1.
Un autovalor mide cuánta varianza explica un componente. Como nuestras variables están estandarizadas (con varianza = 1), un componente con un autovalor menor que 1 estaría explicando menos información que una sola de las variables originales. ¡No sería una buena reducción!
Para ver los autovalores, ejecutamos la función principal() sin especificar nfactors. Por defecto, nos mostrará la solución completa.
# Ejecutamos un ACP inicial sin rotación y sin fijar el número de factores
# para inspeccionar los autovalores.
solucion_completa <- principal(data02, rotate = "none")
# La información clave está en los autovalores (Eigenvalues)
print(solucion_completa$values) [1] 3.42697133 2.55089671 1.69097648 1.08655606 0.60942409 0.55188378
[7] 0.40151815 0.24695154 0.20355327 0.13284158 0.09842702Análisis de los autovalores: La salida nos muestra una lista de los autovalores para cada posible componente, ordenados de mayor a menor. Si los contamos, vemos que el Componente 5 ya toma un valor de solucion_completa$values[5] que es menor que 1.
Claramente, hay 4 componentes que cumplen el Criterio de Kaiser. Esta será nuestra elección para el modelo final. El gráfico de sedimentación (Scree Plot) que veremos más adelante nos ayudará a confirmar visualmente esta decisión.
5.4.2 3.2. Primer modelo rotado y el problema de las cargas cruzadas
Ahora que hemos justificado la elección de 4 componentes, volvemos a ejecutar el análisis, pero esta vez especificando nfactors = 4 y añadiendo la rotación varimax para que la solución sea fácilmente interpretable.
# Ejecutamos el ACP sobre el set de datos 'data02' con 4 factores y rotación
output_preliminar <- principal(data02, nfactors = 4, rotate = "varimax")
print(output_preliminar, cut = 0, digits = 2, n=99)Principal Components Analysis
Call: principal(r = data02, nfactors = 4, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 RC3 RC4 h2 u2 com
x6 0.00 -0.01 -0.03 0.88 0.77 0.232 1.0
x7 0.06 0.87 0.05 -0.12 0.78 0.223 1.1
x8 0.02 -0.02 0.94 0.10 0.89 0.107 1.0
x9 0.93 0.12 0.05 0.09 0.88 0.119 1.1
x10 0.14 0.74 -0.08 0.01 0.58 0.424 1.1
x11 0.59 -0.06 0.15 0.64 0.79 0.213 2.1
x12 0.13 0.90 0.08 -0.16 0.86 0.141 1.1
x13 -0.09 0.23 -0.25 -0.72 0.64 0.359 1.5
x14 0.11 0.05 0.93 0.10 0.89 0.108 1.1
x16 0.86 0.11 0.08 0.04 0.77 0.234 1.1
x18 0.94 0.18 0.00 0.05 0.91 0.086 1.1
RC1 RC2 RC3 RC4
SS loadings 2.89 2.23 1.86 1.77
Proportion Var 0.26 0.20 0.17 0.16
Cumulative Var 0.26 0.47 0.63 0.80
Proportion Explained 0.33 0.26 0.21 0.20
Cumulative Proportion 0.33 0.59 0.80 1.00
Mean item complexity = 1.2
Test of the hypothesis that 4 components are sufficient.
The root mean square of the residuals (RMSR) is 0.06
with the empirical chi square 39.02 with prob < 0.0018
99
Fit based upon off diagonal values = 0.97Cuando observamos la tabla de resultados de la función principal(), además de las cargas factoriales (RC1, RC2, etc.), aparecen tres columnas adicionales a la derecha: h2, u2 y com. Estas columnas nos dan información diagnóstica crucial sobre la calidad de nuestra solución.
5.4.2.1 h2 (Comunalidad)
- ¿Qué es? La comunalidad (
h2) representa la proporción de la varianza de una variable que es explicada por los componentes retenidos. Es un número que va de 0 a 1. - Analogía: Imagina que cada variable tiene una “varianza total” que es como su “potencial de trabajo”. La comunalidad es el porcentaje de ese potencial que la empresa (nuestro modelo factorial) está aprovechando. Es como el “sueldo” que la variable recibe del modelo.
- ¿Cómo se interpreta?
- Una
h2alta (ej. > 0.70) significa que la variable está muy bien representada por nuestra solución. Está “feliz” y bien integrada en los componentes. - Una
h2baja (ej. < 0.50) es una señal de alerta. Significa que menos de la mitad de la información de esa variable está siendo capturada por los componentes. La variable no encaja bien en el modelo y gran parte de su “personalidad” se está perdiendo. Si una variable importante tiene una comunalidad muy baja, podríamos reconsiderar su inclusión.
- Una
5.4.2.2 u2 (Unicidad o Varianza Específica)
- ¿Qué es? La unicidad (
u2) es simplemente lo contrario de la comunalidad. Se calcula como 1 - h2. Representa la proporción de la varianza de una variable que NO es explicada por los componentes. - Analogía: Si
h2es el “sueldo” que la variable aporta al trabajo,u2es la parte de su “potencial” que se queda en casa o que dedica a sus “hobbies privados”. Es la parte de la variable que es única, específica de ella misma, y que no comparte con los demás. - ¿Cómo se interpreta? Es el reverso de la comunalidad. Una
u2alta indica que la variable es un “lobo solitario” con mucha información específica que no se alinea con los factores comunes.
5.4.2.3 com (Complejidad)
- ¿Qué es? La complejidad (
com, de complexity) mide en cuántos componentes carga significativamente una variable. - Analogía: Es el “índice de pluriempleo” de una variable.
- Un valor de
comcercano a 1 es ideal. Significa que la variable trabaja casi exclusivamente para un solo componente. Tiene un “jefe” claro y su rol es fácil de interpretar. - Un valor de
comde 2 o más es un problema. Significa que la variable está “pluriempleada”, trabajando para dos o más componentes a la vez. Esto es la definición de una carga cruzada. Una variable con alta complejidad es difícil de interpretar y “ensucia” la estructura factorial.
- Un valor de
- ¿Cómo se interpreta? Esta columna nos ayuda a detectar numéricamente las cargas cruzadas que antes identificábamos visualmente. Si una variable tiene un valor de
comelevado (ej. > 1.8), es una candidata a ser problemática, como lo fuex11en nuestro análisis.
En resumen, al mirar estas tres columnas, buscamos variables con h2 alta, u2 baja y com cercana a 1. Esas son las “empleadas modelo” de nuestro análisis factorial.
5.5 3. Extracción e interpretación de componentes
Ahora llega el momento de la verdad. Vamos a ejecutar el ACP. Usaremos la función principal() del paquete psych. Le pedimos que extraiga 4 componentes (basado en el criterio de autovalor > 1 que vimos en clase) y que aplique una rotación varimax para facilitar la interpretación.
5.5.1 3.1. Primer modelo y el problema de las cargas cruzadas
# Ejecutamos el ACP sobre el set de datos 'data02'
output_preliminar <- principal(data02, nfactors = 4, rotate = "varimax")
print(output_preliminar, cut = 0, digits = 2)Principal Components Analysis
Call: principal(r = data02, nfactors = 4, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 RC3 RC4 h2 u2 com
x6 0.00 -0.01 -0.03 0.88 0.77 0.232 1.0
x7 0.06 0.87 0.05 -0.12 0.78 0.223 1.1
x8 0.02 -0.02 0.94 0.10 0.89 0.107 1.0
x9 0.93 0.12 0.05 0.09 0.88 0.119 1.1
x10 0.14 0.74 -0.08 0.01 0.58 0.424 1.1
x11 0.59 -0.06 0.15 0.64 0.79 0.213 2.1
x12 0.13 0.90 0.08 -0.16 0.86 0.141 1.1
x13 -0.09 0.23 -0.25 -0.72 0.64 0.359 1.5
x14 0.11 0.05 0.93 0.10 0.89 0.108 1.1
x16 0.86 0.11 0.08 0.04 0.77 0.234 1.1
x18 0.94 0.18 0.00 0.05 0.91 0.086 1.1
RC1 RC2 RC3 RC4
SS loadings 2.89 2.23 1.86 1.77
Proportion Var 0.26 0.20 0.17 0.16
Cumulative Var 0.26 0.47 0.63 0.80
Proportion Explained 0.33 0.26 0.21 0.20
Cumulative Proportion 0.33 0.59 0.80 1.00
Mean item complexity = 1.2
Test of the hypothesis that 4 components are sufficient.
The root mean square of the residuals (RMSR) is 0.06
with the empirical chi square 39.02 with prob < 0.0018
Fit based upon off diagonal values = 0.97Análisis de la tabla: La tabla nos muestra las “cargas” de cada variable en los 4 componentes (RC1, RC2, etc.). Una carga es la correlación de la variable con el componente. Para una interpretación limpia, cada variable debería tener una carga alta en un solo componente.
Aquí detectamos un problema:
- Variable
x11(Línea de producto): Tiene una carga alta en el componente 1 (0.59) y también en el componente 4 (0.64). No tiene una “lealtad” clara, lo que se conoce como carga cruzada. Esto ensucia la interpretación y nos sugiere quex11podría no encajar bien en esta estructura. Además, en la columna com, nótese su valor de 2.12, lo que nos da idea de estar en más de una componente.
Decisión: Para obtener una solución final más clara y robusta, decidimos eliminar x11 y volver a ejecutar todo el proceso.
5.6 4. La solución final
Repetimos los pasos de diagnóstico con nuestro último set de datos, ahora sin x11.
# Creamos el dataframe definitivo
data03 <- subset(data02, select = -c(x11))
# Re-validamos KMO y Bartlett (buena práctica)
print("KMO Final:")[1] "KMO Final:"KMO(data03)Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = data03)
Overall MSA = 0.67
MSA for each item =
x6 x7 x8 x9 x10 x12 x13 x14 x16 x18
0.61 0.64 0.52 0.69 0.81 0.63 0.74 0.53 0.83 0.72 print("Bartlett Final:")[1] "Bartlett Final:"cortest.bartlett(data03)$chisq
[1] 502.9739
$p.value
[1] 1.130404e-78
$df
[1] 45Diagnóstico final: El KMO sigue siendo bueno (0.72) y el test de Bartlett sigue siendo significativo. Tenemos un conjunto de 10 variables robusto y adecuado.
5.6.1 4.1. Modelo ACP definitivo
Ejecutamos el ACP por última vez sobre nuestro conjunto de datos depurado.
# Modelo final con el set de datos 'data03'
output_final <- principal(data03, nfactors = 4, rotate = "varimax")
# Mostramos los resultados, omitiendo cargas pequeñas para mayor claridad
print(output_final, cut = 0.3, digits = 3)Principal Components Analysis
Call: principal(r = data03, nfactors = 4, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 RC3 RC4 h2 u2 com
x6 0.892 0.798 0.202 1.00
x7 0.868 0.780 0.220 1.07
x8 0.940 0.894 0.106 1.02
x9 0.933 0.890 0.110 1.05
x10 0.743 0.585 0.415 1.12
x12 0.898 0.860 0.140 1.13
x13 -0.730 0.661 0.339 1.50
x14 0.933 0.891 0.109 1.05
x16 0.886 0.806 0.194 1.06
x18 0.931 0.894 0.106 1.06
RC1 RC2 RC3 RC4
SS loadings 2.589 2.216 1.846 1.406
Proportion Var 0.259 0.222 0.185 0.141
Cumulative Var 0.259 0.481 0.665 0.806
Proportion Explained 0.321 0.275 0.229 0.175
Cumulative Proportion 0.321 0.596 0.825 1.000
Mean item complexity = 1.1
Test of the hypothesis that 4 components are sufficient.
The root mean square of the residuals (RMSR) is 0.063
with the empirical chi square 35.712 with prob < 0.000189
Fit based upon off diagonal values = 0.9625.6.2 4.2. Interpretación y nominación de los componentes
Ahora, interpretamos la matriz de componentes rotados. Agrupamos las variables que cargan fuertemente en cada componente y le damos un nombre de marketing que resuma su significado.
- Componente 1 (RC1): Servicio Postventa y Operaciones
x9(Resolución de quejas): 0.848x18(Rapidez de entrega): 0.808x16(Pedidos y facturación): 0.761 Este componente agrupa todas las percepciones relacionadas con la eficiencia y la capacidad de respuesta de la empresa una vez realizada la venta.
- Componente 2 (RC2): Actividad Comercial y de Marketing
x12(Imagen de los vendedores): 0.841x7(Actividades e-Commerce): 0.789x10(Publicidad): 0.739 Este componente captura la imagen que proyecta la empresa a través de su fuerza de ventas, su presencia online y sus esfuerzos publicitarios.
- Componente 3 (RC3): Soporte y Fiabilidad del Servicio
x8(Apoyo técnico): 0.860x14(Garantía): 0.838 Este componente se centra en la confianza que genera la empresa a través de su soporte técnico y el cumplimiento de sus promesas.
- Componente 4 (RC4): Propuesta de Valor del Producto
x6(Calidad del producto): 0.870x13(Competitividad de los precios): 0.829 Este componente refleja los dos atributos más fundamentales del producto en sí: su calidad intrínseca y su precio en el mercado.
Varianza explicada: En la parte inferior de la tabla, vemos que estos 4 componentes explican en conjunto el 73% de la varianza total de las 10 variables originales. Hemos logrado una excelente reducción de datos perdiendo muy poca información.
5.7 5. Visualización de resultados con factoextra
Si bien el paquete psych es excelente para el cálculo e interpretación tabular, el paquete factoextra nos ofrece herramientas de visualización superiores basadas en ggplot2. Para asegurar la compatibilidad, recalcularemos nuestro ACP final utilizando la función prcomp() de R base, que es el estándar de facto para este tipo de análisis.
5.7.1 5.1. Paso 1: Recalcular el ACP con una función compatible
Ejecutamos prcomp() sobre nuestro data frame final y depurado (data03). Es fundamental usar el argumento scale. = TRUE para que todas las variables se estandaricen antes del análisis, asegurando que ninguna domine los resultados solo por tener una escala mayor.
library(factoextra)
# Recalculamos el ACP usando prcomp() para la compatibilidad con factoextra
# Usamos el dataframe final 'data03'
pca_final <- prcomp(data03, scale. = TRUE)
# Podemos ver un resumen del objeto creado
summary(pca_final)Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.7567 1.5077 1.2881 1.0192 0.77724 0.74069 0.54092
Proportion of Variance 0.3086 0.2273 0.1659 0.1039 0.06041 0.05486 0.02926
Cumulative Proportion 0.3086 0.5359 0.7018 0.8057 0.86613 0.92099 0.95025
PC8 PC9 PC10
Standard deviation 0.45408 0.41369 0.34669
Proportion of Variance 0.02062 0.01711 0.01202
Cumulative Proportion 0.97087 0.98798 1.000005.7.2 5.2. Paso 2: El gráfico de sedimentación (Scree Plot) correcto
Ahora, con el objeto pca_final, podemos usar fviz_eig() (o fviz_screeplot()) de factoextra para crear un gráfico de sedimentación claro y profesional. Este gráfico es la herramienta visual clave para aplicar la “regla del codo” y justificar el número de componentes a retener.
# Creamos el gráfico de sedimentación con factoextra
fviz_eig(pca_final,
addlabels = TRUE,
ylim = c(0, 50),
main = "Gráfico de Sedimentación (Scree Plot)",
barfill = "steelblue",
barcolor = "steelblue") +
labs(title = "Gráfico de Sedimentación (Scree Plot)",
x = "Componentes Principales",
y = "% de Varianza Explicada") +
theme_minimal()+
ggthemes::theme_economist()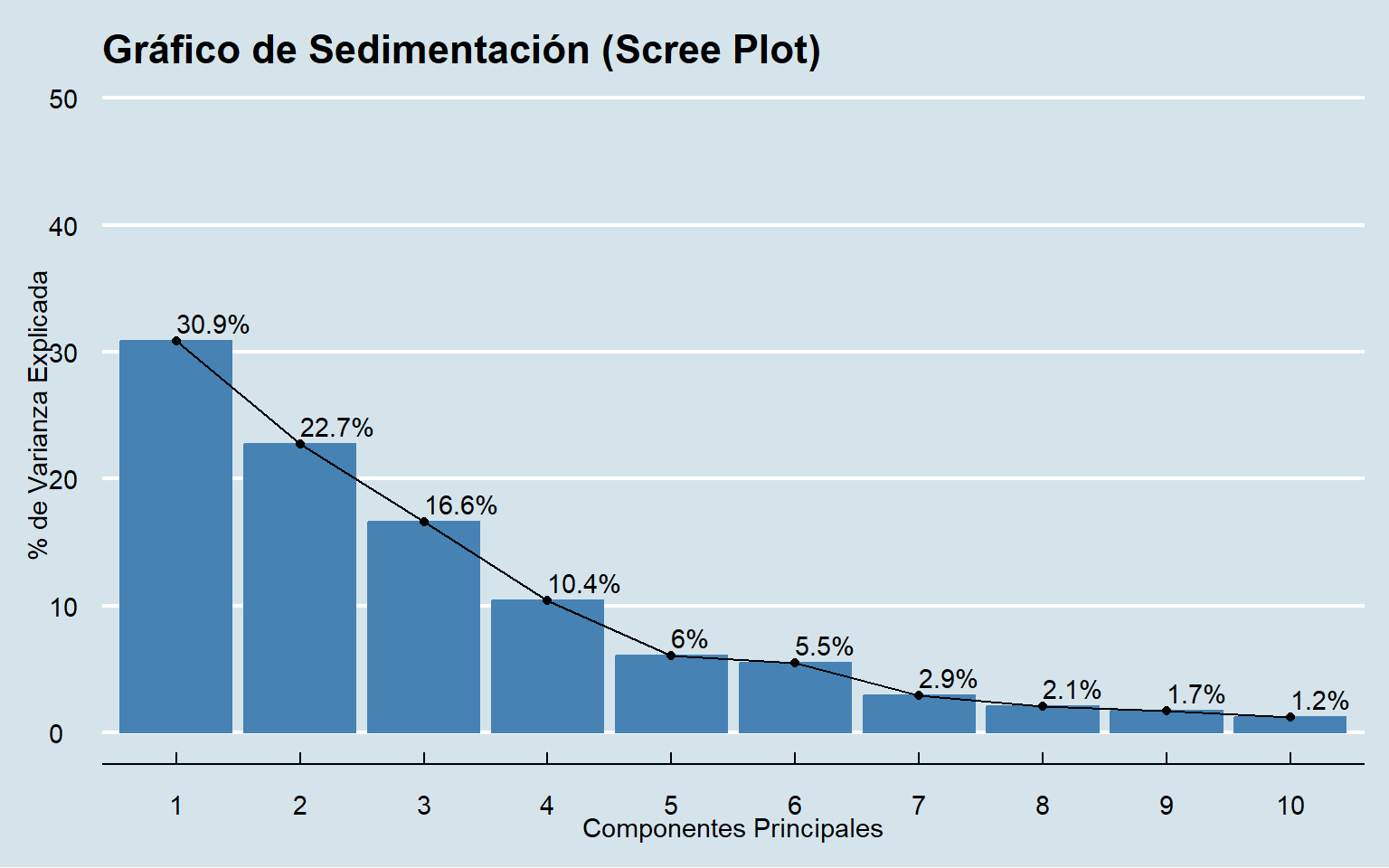
Interpretación: Este gráfico confirma visualmente nuestra decisión anterior. Vemos una caída muy pronunciada después del primer componente y luego caídas más suaves hasta el cuarto. A partir del quinto componente, la línea se aplana considerablemente. El “codo” se sitúa en el componente 5, lo que refuerza la decisión de retener los 4 anteriores.
5.7.3 5.3. Paso 3: El mapa perceptual (Biplot de variables)
Esta es una de las visualizaciones más potentes. Un biplot nos muestra las variables originales como vectores (flechas) en el nuevo espacio dimensional creado por los componentes.
- Vectores cercanos (ángulo pequeño): Indican variables que están positivamente correlacionadas.
- Vectores opuestos (180 grados): Indican variables negativamente correlacionadas.
- Vectores perpendiculares (90 grados): Indican variables que no tienen correlación.
- Longitud del vector: Representa la calidad con la que la variable es representada en el mapa 2D. Vectores más largos están mejor representados.
# Gráfico de las variables en el espacio de los componentes
fviz_pca_var(pca_final,
col.var = "contrib", # Colorear por contribución al mapa
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Evitar solapamiento de etiquetas
ggtheme = theme_minimal()) +
labs(title = "Mapa Perceptual de Variables",
subtitle = "Basado en los dos primeros componentes principales")+
ggthemes::theme_economist()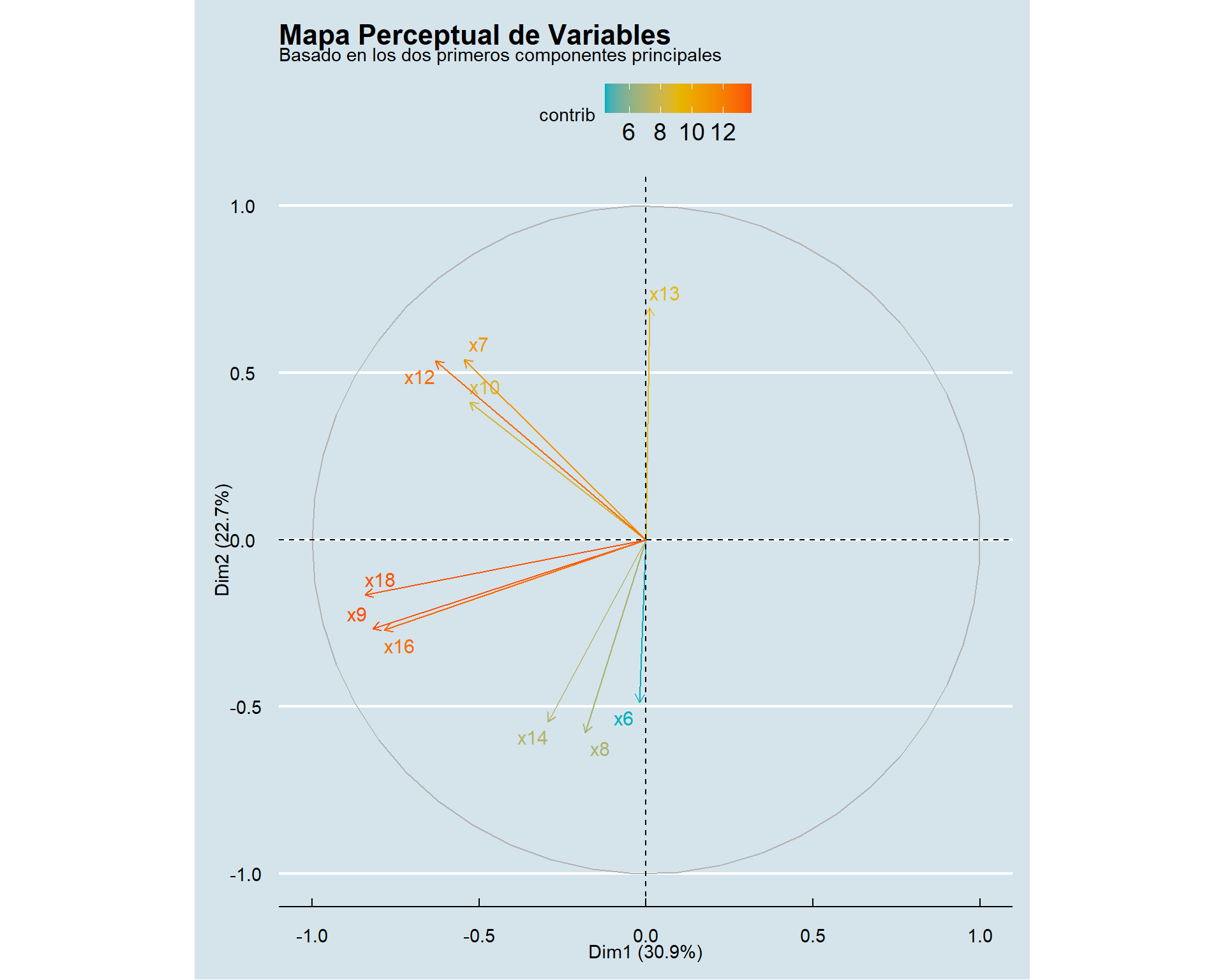
Interpretación: Este mapa cuenta la historia de forma visual. Vemos claramente los 4 grupos de variables que identificamos en la tabla:
- Grupo Postventa (abajo a la izquierda):
x9,x18,x16aparecen juntas. - Grupo Comercial (arriba a la izquierda):
x12,x7,x10forman otro clúster. - Grupo Soporte (arriba a la derecha):
x8yx14están muy unidas. - Grupo Producto (abajo a la derecha):
x6yx13forman el último par.
5.7.4 5.4. Paso 4 (Opcional pero recomendado): Gráfico de contribuciones
Finalmente, podemos visualizar qué variables contribuyen más a la creación de cada una de las dimensiones. Esto nos ayuda a confirmar el nombre que le dimos a cada componente.
# Gráfico de contribución de las variables a la Dimensión 1
p1 <- fviz_contrib(pca_final, choice = "var", axes = 1, top = 10)+
ggthemes::theme_economist()
# Gráfico de contribución de las variables a la Dimensión 2
p2 <- fviz_contrib(pca_final, choice = "var", axes = 2, top = 10)+
ggthemes::theme_economist()
# Unir los dos gráficos
gridExtra::grid.arrange(p1, p2, ncol = 2)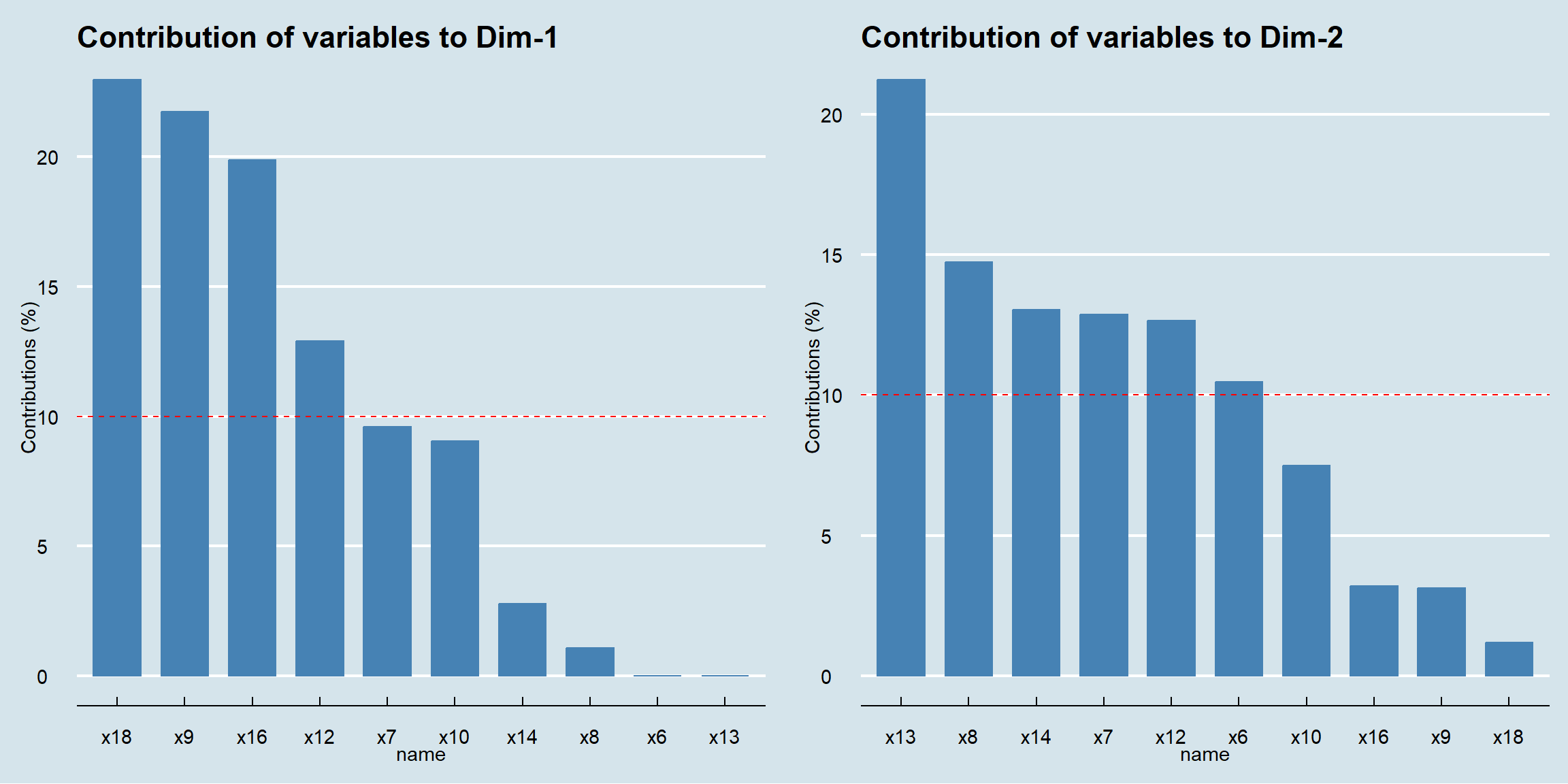
Interpretación: El gráfico de la izquierda nos muestra que las variables que más definen el eje horizontal (Dimensión 1) son las de Soporte y Producto. El gráfico de la derecha muestra que el eje vertical (Dimensión 2) está definido principalmente por las variables de Actividad Comercial y Servicio Postventa. Esto nos da una comprensión más profunda de la estructura de nuestro mercado perceptual.