6  Análisis de clúster

Segmentando a los clientes de la empresa HATCO con R

Published

November 22, 2025

6.1 Introducción

Imagina que eres el director de marketing de HATCO. Tienes una base de datos con las percepciones de 100 de tus clientes sobre 7 atributos clave de tu servicio, desde la rapidez de entrega hasta la calidad del producto. Mirar los datos de 100 clientes a la vez es abrumador.

La pregunta estratégica es: ¿Son todos nuestros clientes iguales? ¿O existen grupos naturales con necesidades y percepciones diferentes?

El análisis de clúster es nuestra herramienta de “visión de rayos X” para responder a esta pregunta. Nos permitirá pasar de una masa de 100 clientes individuales a un número reducido de segmentos de mercado claros, homogéneos por dentro y diferentes entre sí.

El objetivo de este análisis es:

  1. Descubrir: Identificar si existen grupos naturales de clientes.
  2. Caracterizar: Entender qué define a cada grupo en función de los atributos de servicio.
  3. Perfilar: Describir a cada grupo utilizando otras variables demográficas o de comportamiento para hacerlos “accionables”.

Este documento te guiará a través del proceso completo, desde la preparación de los datos hasta la creación de “personas” de marketing para cada segmento.

6.2 Fase 1: Preparación de los datos

El primer paso es siempre preparar nuestro “terreno de juego”.

6.2.1 1.1. Selección de variables y estandarización

Seleccionamos las 7 variables de percepción (x1 a x7) que usaremos para segmentar. Es crucial que todas las variables estén en la misma escala para que ninguna domine el análisis solo por tener números más grandes. En este caso, todas están en una escala de 0-10, por lo que no es estrictamente necesario estandarizar.

# Seleccionamos las variables para el clustering
data_cluster <- select(hatco, X1:X7)

# Estandarizaríamos las variables (convertirlas a puntuaciones Z) si fuera necesario
#data_scaled <- scale(data_cluster)

6.2.2 1.2. Detección de outliers

El análisis de clúster es sensible a los outliers, ya que un solo caso muy extremo puede distorsionar la formación de un grupo o incluso crear un “segmento de uno”. Usamos la distancia de Mahalanobis para detectar outliers multivariantes.

Analogía: La distancia de Mahalanobis es como un “detector de rareza”. No mira cada variable por separado, sino que evalúa cuán “extraña” es la combinación de valores de un cliente en comparación con el resto.

# Calculamos la distancia de Mahalanobis para cada caso
mh <- mahalanobis(data_cluster, center = colMeans(data_cluster), cov = cov(data_cluster))

# Calculamos el p-valor asociado (distribución Chi-cuadrado)
# df = número de variables
pmh <- pchisq(mh, df = 7, lower.tail = FALSE)

# Regla de oro: eliminamos casos con p < .001 (un criterio muy estricto)
outliers_a_eliminar <- which(pmh < 0.001)

# Creamos nuestro dataframe final sin outliers
if (length(outliers_a_eliminar) > 0) {
  data_final <- data_cluster[-outliers_a_eliminar, ]
  hatco_final <- hatco[-outliers_a_eliminar, ]
} else {
  data_final <- data_scaled
  hatco_final <- hatco
}

cat("Número de outliers detectados y eliminados:", length(outliers_a_eliminar))
Número de outliers detectados y eliminados: 2

6.3 Fase 2: Exploración - El Clúster Jerárquico

Nuestra primera misión es exploratoria. No sabemos cuántos segmentos hay. El clúster jerárquico nos dibujará un “mapa familiar” o dendrograma que nos sugerirá el número más probable de grupos.

# 1. Calculamos la matriz de distancias euclídeas entre todos los clientes
distancias <- dist(data_final, method = "euclidean")

# 2. Ejecutamos el clustering jerárquico (método de Ward.D2 es robusto)
clust_jerarquico <- hclust(distancias, method = "ward.D2")

# 3. Visualizamos el dendrograma
plot(clust_jerarquico, main = "Dendrograma de Clientes de HATCO", xlab = "", sub = "")
# Añadimos un rectángulo para sugerir una solución de 2 clústeres
rect.hclust(clust_jerarquico, k = 2, border = "red")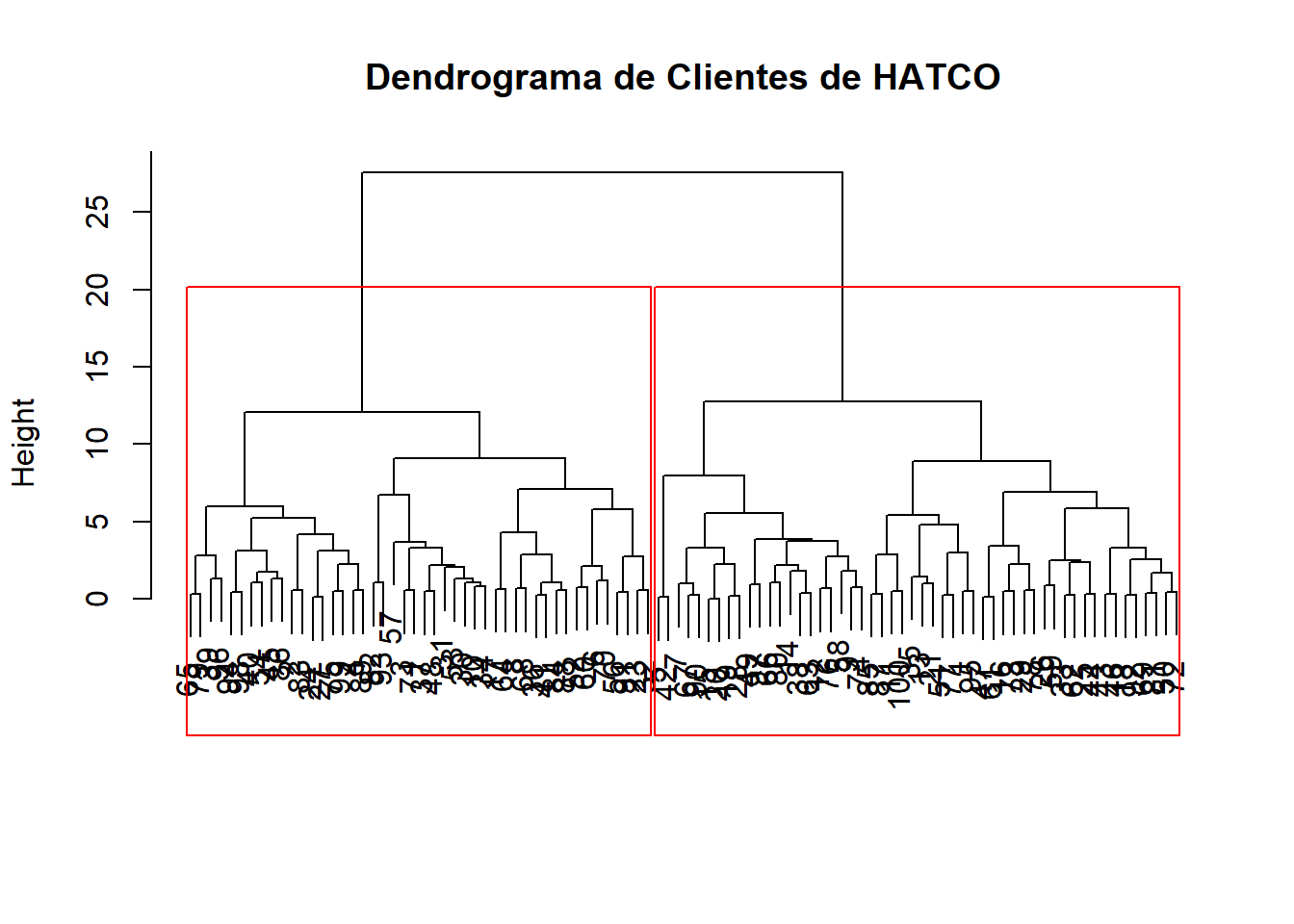

Interpretación del dendrograma: El eje vertical representa la distancia a la que se unen los grupos. Buscamos “saltos” verticales grandes. Un salto grande significa que estamos uniendo dos grupos que eran muy diferentes entre sí. En este caso, el salto más grande se produce al pasar de 2 grupos a 1, lo que sugiere que una solución de 2 clústeres es la más natural y robusta.

6.4 Fase 3: Decisión - ¿Cuál es el número óptimo de clústeres?

Aunque el dendrograma es útil, podemos usar un método más sofisticado para confirmar nuestra decisión. El paquete NbClust es como un “comité de expertos”: aplica hasta 30 índices estadísticos diferentes y vota por el mejor número de clústeres.

# Ejecutamos NbClust (puede tardar un poco)
# Le pedimos que evalúe entre 2 y 5 clústeres
set.seed(123)
res_nbclust <- NbClust(data_final, distance = "euclidean", min.nc = 2, max.nc = 5, 
                       method = "ward.D2", index = "all")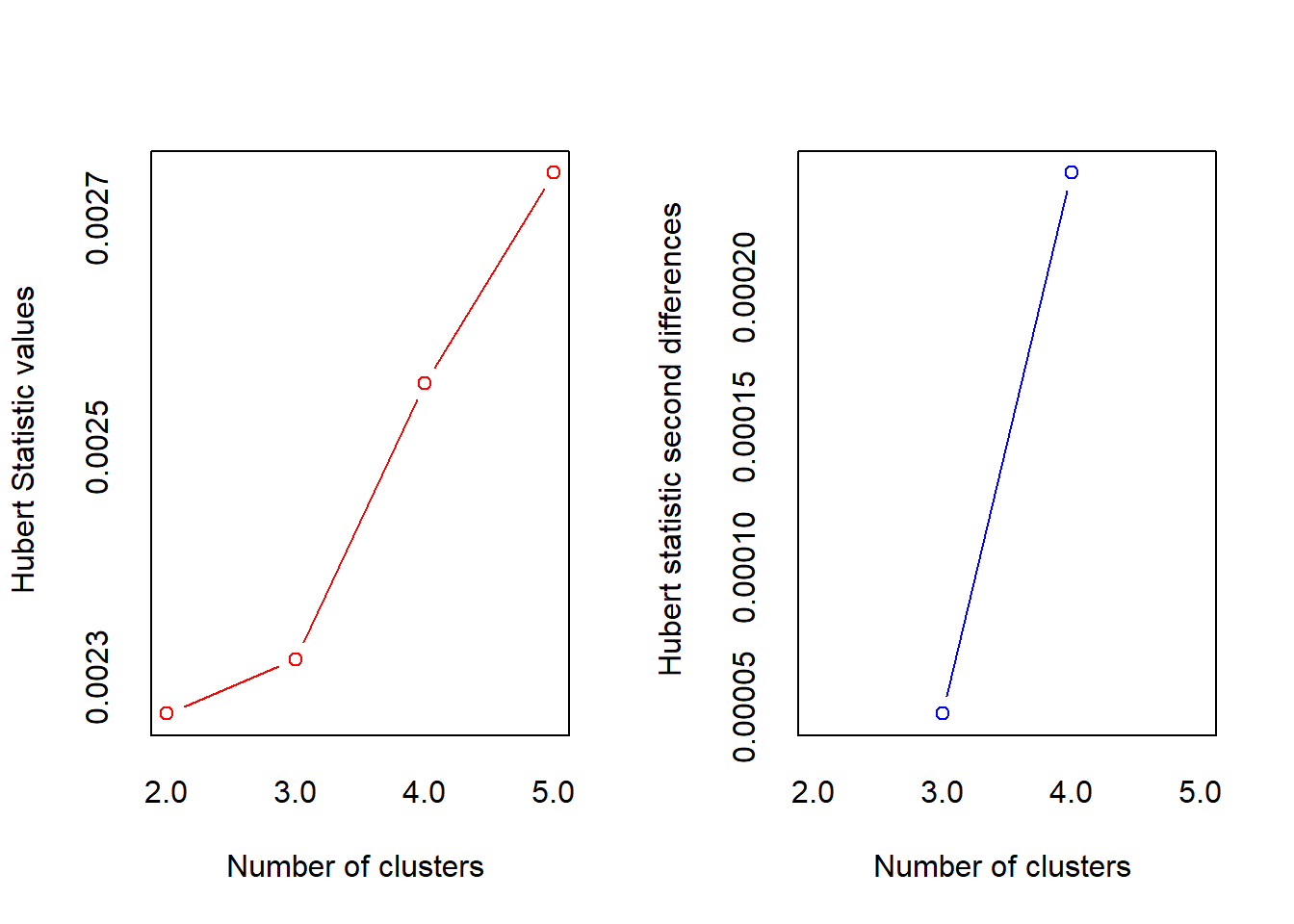

*** : The Hubert index is a graphical method of determining the number of clusters.
                In the plot of Hubert index, we seek a significant knee that corresponds to a 
                significant increase of the value of the measure i.e the significant peak in Hubert
                index second differences plot. 
 

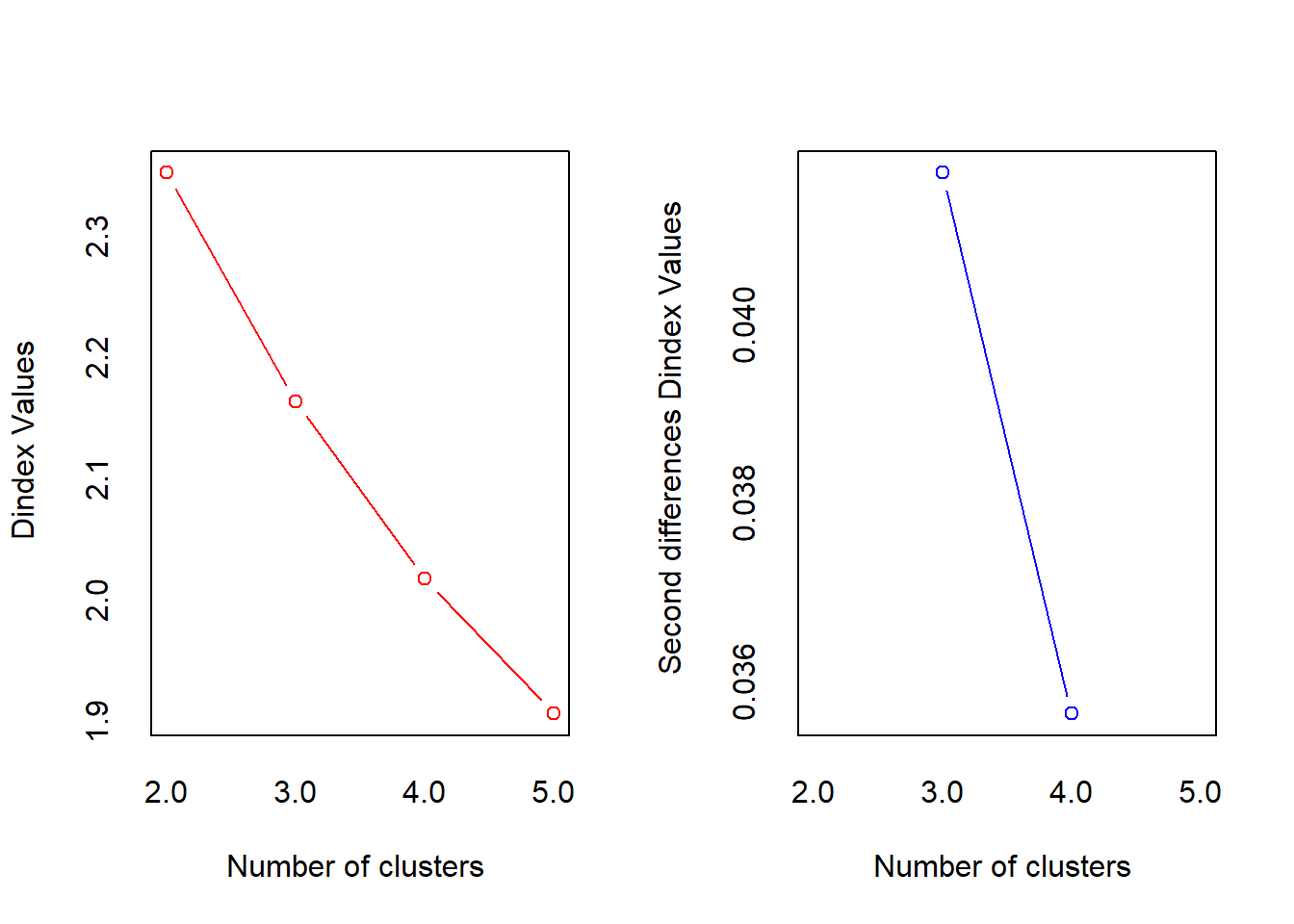
*** : The D index is a graphical method of determining the number of clusters. 
                In the plot of D index, we seek a significant knee (the significant peak in Dindex
                second differences plot) that corresponds to a significant increase of the value of
                the measure. 
 
******************************************************************* 
* Among all indices:                                                
* 13 proposed 2 as the best number of clusters 
* 3 proposed 3 as the best number of clusters 
* 6 proposed 4 as the best number of clusters 
* 2 proposed 5 as the best number of clusters 

                   ***** Conclusion *****                            
 
* According to the majority rule, the best number of clusters is  2 
 
 
*******************************************************************

Diagnóstico: El resultado de NbClust es claro. La gran mayoría de los índices estadísticos coinciden en que el número óptimo de clústeres es 2. Con la evidencia del dendrograma y la confirmación de NbClust, tenemos una gran confianza para proceder con una solución de dos segmentos.

6.5 Fase 4: Confirmación - El Clúster K-Means

Ahora que sabemos que buscamos 2 segmentos, usamos el método K-Means para obtener la solución final. K-Means es más robusto que el jerárquico una vez que el número de grupos está definido.

# Ejecutamos K-Means pidiendo 2 clústeres
# nstart=25 ejecuta el algoritmo 25 veces con inicios aleatorios y se queda con la mejor solución
set.seed(123)
clust_kmeans <- kmeans(data_final, centers = 2, nstart = 25)

# Añadimos la asignación de clúster a nuestro dataframe original
hatco_final$segmento_kmeans <- as.factor(clust_kmeans$cluster)

6.6 Fase 5: Caracterización de los Segmentos

Ya tenemos los grupos. Ahora, la pregunta es: ¿En qué se diferencian? Para ello, comparamos las puntuaciones medias de cada segmento en las 7 variables que usamos para crearlos.

# Usamos expss para crear una tabla de medias por segmento
hatco_final %>%
  tab_cells(X1, X2, X3, X4, X5, X6, X7) %>%
  tab_cols(segmento_kmeans) %>%
  tab_stat_mean_sd_n() %>%
  tab_last_sig_means() %>% # Añade un test t para ver si las diferencias son significativas
  tab_pivot() %>% 
  set_caption("Caracterización de los Segmentos (Medias)")
Caracterización de los Segmentos (Medias)
 segmento_kmeans 
 1     2 
 A     B 
 rapidez de servicio 
   Mean  4.4 B   2.6  
   Std. dev.  1.0     1.0  
   Unw. valid N  50.0     48.0  
 nivel de precios 
   Mean  1.6     3.2 A
   Std. dev.  0.6     1.1  
   Unw. valid N  50.0     48.0  
 flexibilidad de precios 
   Mean  8.9 B   6.8  
   Std. dev.  0.8     1.0  
   Unw. valid N  50.0     48.0  
 imagen del fabricante 
   Mean  5.0     5.6 A
   Std. dev.  1.1     1.0  
   Unw. valid N  50.0     48.0  
 servicio 
   Mean  3.0     2.9  
   Std. dev.  0.6     0.9  
   Unw. valid N  50.0     48.0  
 imagen de los vendedores 
   Mean  2.6     2.8  
   Std. dev.  0.9     0.6  
   Unw. valid N  50.0     48.0  
 calidad del producto 
   Mean  5.9     8.1 A
   Std. dev.  1.3     1.0  
   Unw. valid N  50.0     48.0  

Interpretación y “Bautizo” de los Segmentos: La tabla nos muestra diferencias muy claras y estadísticamente significativas.

  • Segmento 1: “Los Pragmáticos del Precio” (N = 50)
    • Este grupo valora muy positivamente el Nivel de Precios (x2) y la Flexibilidad de Precios (x3).
    • Sin embargo, son muy críticos con la Calidad del Servicio (x5) y la Rapidez de Entrega (x1).
    • Son clientes para los que el factor económico es lo más importante, y parecen estar dispuestos a sacrificar calidad de servicio por un buen precio.
  • Segmento 2: “Los Exigentes de la Calidad” (N = 48)
    • Este grupo muestra el patrón opuesto. Valoran excepcionalmente bien la Calidad del Servicio (x5) y la Rapidez de Entrega (x1).
    • Por otro lado, son muy críticos con el Nivel de Precios (x2) y la Flexibilidad de Precios (x3).
    • Son clientes que buscan la máxima calidad y están dispuestos a pagar por ella. La eficiencia y la excelencia en el servicio son sus prioridades.

6.7 Fase 6: Perfilado de los Segmentos

Sabemos qué piensan, pero ahora necesitamos saber quiénes son. Para ello, cruzamos nuestros segmentos con otras variables del dataset (tipo de industria, región, etc.) para ver si hay perfiles demográficos o de comportamiento distintivos.

# Usamos expss para crear tablas de contingencia con test Chi-cuadrado
hatco_final %>%
  tab_cells(X8, X11, X12, X13, X14) %>% # Variables categóricas de perfilado
  tab_cols(total(), segmento_kmeans) %>%
  tab_stat_cpct() %>% # Porcentajes columna
  tab_last_sig_cases() %>% # Añade un test Chi-cuadrado
  tab_pivot() %>% 
  set_caption("Perfilado de los Segmentos (Variables Categóricas)")
Perfilado de los Segmentos (Variables Categóricas)
 #Total     segmento_kmeans 
   1   2 
 tamaño de la empresa 
   pequeña  59.18367    96.0  20.83333 
   grande  40.81633    4.0  79.16667 
   #Chi-squared p-value    <0.05 
   #Total cases  98.0    50.0  48.0 
 especificación de las compras 
   especificacion  40.81633    4.0  79.16667 
   valor total  59.18367    96.0  20.83333 
   #Chi-squared p-value    <0.05 
   #Total cases  98.0    50.0  48.0 
 estructura 
   descentralizada  48.97959    96.0 
   centralizada  51.02041    4.0  100.0 
   #Chi-squared p-value    <0.05 
   #Total cases  98.0    50.0  48.0 
 tipo de industria 
   tipo 1  48.97959    52.0  45.83333 
   tipo 2  51.02041    48.0  54.16667 
   #Chi-squared p-value   
   #Total cases  98.0    50.0  48.0 
 situacion de compra 
   nueva  32.65306    16.0  50.000000 
   recompra modificada  32.65306    20.0  45.833333 
   recompra  34.69388    64.0  4.166667 
   #Chi-squared p-value    <0.05 
   #Total cases  98.0    50.0  48.0 

Interpretación del Perfil: Al analizar las tablas de perfilado, podríamos encontrar (dependiendo de los datos) patrones como:

  • Tipo de Industria (x8): Quizás “Los Exigentes de la Calidad” se concentran en una industria donde la rapidez es crítica, mientras que “Los Pragmáticos del Precio” están en sectores con márgenes más ajustados.
  • Región (x11): Podría haber diferencias geográficas en las expectativas de los clientes.
  • Estructura de Compra (x13): Tal vez los clientes con una estructura de compra centralizada son más sensibles al precio.

Estos insights son oro puro para el equipo de ventas y marketing, ya que permiten adaptar las estrategias comerciales a cada segmento.

6.8 Fase 7: Análisis de Estabilidad (Opcional pero recomendado)

Como último paso, podemos comprobar si la solución de K-Means es similar a la que hubiéramos obtenido con el método jerárquico. Una alta coincidencia nos da más confianza en la robustez de nuestros segmentos.

# Asignamos los clústeres de la solución jerárquica de 2 grupos
hatco_final$segmento_jerarquico <- as.factor(cutree(clust_jerarquico, k = 2))

# Creamos una tabla de contingencia para comparar ambas soluciones
tabla_cruzada <- table(
  `K-Means` = hatco_final$segmento_kmeans,
  `Jerárquico` = hatco_final$segmento_jerarquico
)

# Calculamos el Adjusted Rand Index (ARI)
# Un valor cercano a 1 indica una concordancia casi perfecta.
# Un valor cercano a 0 indica que la concordancia es la esperada por azar.
ari <- adjustedRandIndex(hatco_final$segmento_kmeans, hatco_final$segmento_jerarquico)

print("Tabla de Concordancia entre Métodos:")
[1] "Tabla de Concordancia entre Métodos:"
print(tabla_cruzada)
       Jerárquico
K-Means  1  2
      1 50  0
      2  2 46
cat("\nAdjusted Rand Index (ARI):", round(ari, 3))

Adjusted Rand Index (ARI): 0.919

Conclusión de Estabilidad: Un ARI alto (típicamente > 0.8) nos indica que ambos métodos, a pesar de funcionar de forma diferente, han llegado a una conclusión muy similar sobre quién pertenece a cada grupo. Esto nos da una gran seguridad de que los segmentos que hemos identificado son reales y estables, y no un simple artefacto del algoritmo utilizado.