1 Exploración de Datos y Validación de Supuestos en R

Published

November 22, 2025

1.1 Introducción

Bienvenido a la guía fundamental de análisis de datos en R. Este documento, que hemos llamado “Punto 0”, cubre el paso más crucial de cualquier proyecto de investigación: la exploración inicial de los datos y la validación de los supuestos estadísticos. Antes de poder aplicar técnicas de inferencia como el test t o el ANOVA, debemos entender a fondo nuestras variables y comprobar si cumplen con los requisitos de las pruebas paramétricas.

A lo largo de este documento, replicaremos los procedimientos que tradicionalmente se realizan en SPSS, demostrando la sintaxis y las capacidades de R y RStudio. Nuestro objetivo es construir una base sólida para los análisis más avanzados que realizaremos en las siguientes sesiones.

Primero, cargamos los paquetes que necesitaremos. tidyverse es una colección de paquetes para la manipulación y visualización de datos, haven nos permite leer ficheros de SPSS (.sav), y nortest contiene la prueba de Kolmogorov-Smirnov con la corrección de Lilliefors.

# Instalar paquetes si no los tienes
# install.packages("tidyverse")
# install.packages("haven")
# install.packages("nortest") # Para la prueba de Lilliefors (K-S)
# install.packages("car")     # Para el Test de Levene

library(tidyverse)
library(haven)
library(nortest)
library(car)
library(expss)

1.2 1. Carga y Exploración Inicial del Fichero de Datos

En SPSS, abriríamos un fichero .sav a través del menú. En R, podemos hacer lo mismo de forma programática, lo que garantiza la reproducibilidad de nuestro análisis. Usaremos el fichero gssnet2.sav que se menciona en el material del curso.

# Cargar el fichero de datos de SPSS
# Asegúrate de que el fichero "gssnet2.sav" esté en tu proyecto de RStudio
# o proporciona la ruta completa al archivo.
# Por ejemplo: datos <- read_sav("C:/ruta/a/tus/datos/gssnet2.sav")

# Para este ejemplo, si no tienes el fichero, crearemos datos simulados
# que se parezcan a los del ejemplo (edad y horas de uso de internet por sexo)
# ¡Cuando uses tus datos, reemplaza este bloque con la línea de read_sav!

datos <- read_sav('data/gssnet1.sav')

# Vistazo inicial a los datos (equivalente a la "Vista de Datos" de SPSS)
glimpse(datos)

Rows: 984
Columns: 10
$ age      <dbl+lbl> 30, 39, 72, 41, 24, 23, 27, 34, 45, 51, 46, 56, 46, 23, 5…
$ educ     <dbl+lbl> 11,  9, 10, 13, 12, 12, 12, 10, 11, 12, 12,  6, 10, 10, 1…
$ usecomp  <dbl+lbl> 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, …
$ usenet   <dbl+lbl> 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, …
$ usemail  <dbl+lbl> 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, …
$ emailhrs <dbl+lbl>          NA,          NA,          NA,          NA,  1.00…
$ webhrs   <dbl+lbl>   NA,   NA,   NA,   NA,  2.0,   NA,  0.5,   NA,   NA,   N…
$ nethrs   <dbl+lbl>        NA,        NA,        NA,        NA,  3.000000,   …
$ netcat   <dbl+lbl> NA, NA, NA, NA,  1, NA,  1, NA, NA, NA, NA, NA, NA, NA,  …
$ region   <dbl+lbl> 5, 7, 3, 3, 6, 5, 7, 4, 3, 5, 6, 7, 7, 7, 7, 2, 3, 3, 3, …

# Resumen estadístico rápido de todas las variables
summary(datos)

      age             educ          usecomp           usenet      
 Min.   :18.00   Min.   : 0.00   Min.   :0.0000   Min.   :0.0000  
 1st Qu.:33.00   1st Qu.:12.00   1st Qu.:0.0000   1st Qu.:0.0000  
 Median :45.00   Median :14.00   Median :1.0000   Median :1.0000  
 Mean   :46.25   Mean   :13.74   Mean   :0.7393   Mean   :0.7393  
 3rd Qu.:58.00   3rd Qu.:16.00   3rd Qu.:1.0000   3rd Qu.:1.0000  
 Max.   :89.00   Max.   :20.00   Max.   :1.0000   Max.   :1.0000  
 NA's   :4                       NA's   :6        NA's   :6       
    usemail          emailhrs            webhrs           nethrs         
 Min.   :0.0000   Min.   : 0.01667   Min.   : 0.000   Min.   :  0.08333  
 1st Qu.:0.0000   1st Qu.: 1.00000   1st Qu.: 1.000   1st Qu.:  3.00000  
 Median :1.0000   Median : 2.00000   Median : 4.000   Median :  7.00000  
 Mean   :0.6399   Mean   : 6.09360   Mean   : 6.732   Mean   : 12.82531  
 3rd Qu.:1.0000   3rd Qu.: 7.00000   3rd Qu.: 8.000   3rd Qu.: 15.50000  
 Max.   :1.0000   Max.   :50.00000   Max.   :70.000   Max.   :118.00000  
 NA's   :12       NA's   :367        NA's   :367      NA's   :367        
     netcat          region     
 Min.   :1.000   Min.   :1.000  
 1st Qu.:1.000   1st Qu.:3.000  
 Median :2.000   Median :5.000  
 Mean   :2.361   Mean   :5.117  
 3rd Qu.:3.000   3rd Qu.:7.000  
 Max.   :4.000   Max.   :9.000  
 NA's   :367

1.3 2. Tablas de Frecuencias y Estadísticos Descriptivos

Esta sección replica los procedimientos de Analizar > Estadísticos Descriptivos > Frecuencias y Descriptivos en SPSS.

1.3.1 2.1. Variables Categóricas: Tabla de Frecuencias

Para variables como sex, queremos contar cuántos casos hay en cada categoría.

# Tabla de frecuencias para la variable 'sex'
frecuencias_sexo <- fre(datos$age)

# Mostramos la tabla
knitr::kable(frecuencias_sexo, caption = "Tabla de Frecuencias para Género")

Tabla de Frecuencias para Género
Age of respondent	Count	Valid percent	Percent	Responses, %	Cumulative responses, %
18	10	1.0204082	1.0162602	1.0204082	1.020408
19	10	1.0204082	1.0162602	1.0204082	2.040816
20	6	0.6122449	0.6097561	0.6122449	2.653061
21	13	1.3265306	1.3211382	1.3265306	3.979592
22	9	0.9183673	0.9146341	0.9183673	4.897959
23	18	1.8367347	1.8292683	1.8367347	6.734694
24	26	2.6530612	2.6422764	2.6530612	9.387755
25	21	2.1428571	2.1341463	2.1428571	11.530612
26	20	2.0408163	2.0325203	2.0408163	13.571429
27	17	1.7346939	1.7276423	1.7346939	15.306122
28	22	2.2448980	2.2357724	2.2448980	17.551020
29	12	1.2244898	1.2195122	1.2244898	18.775510
30	19	1.9387755	1.9308943	1.9387755	20.714286
31	17	1.7346939	1.7276423	1.7346939	22.448980
32	19	1.9387755	1.9308943	1.9387755	24.387755
33	23	2.3469388	2.3373984	2.3469388	26.734694
34	24	2.4489796	2.4390244	2.4489796	29.183674
35	24	2.4489796	2.4390244	2.4489796	31.632653
36	12	1.2244898	1.2195122	1.2244898	32.857143
37	13	1.3265306	1.3211382	1.3265306	34.183673
38	22	2.2448980	2.2357724	2.2448980	36.428571
39	13	1.3265306	1.3211382	1.3265306	37.755102
40	27	2.7551020	2.7439024	2.7551020	40.510204
41	17	1.7346939	1.7276423	1.7346939	42.244898
42	17	1.7346939	1.7276423	1.7346939	43.979592
43	19	1.9387755	1.9308943	1.9387755	45.918367
44	24	2.4489796	2.4390244	2.4489796	48.367347
45	19	1.9387755	1.9308943	1.9387755	50.306122
46	26	2.6530612	2.6422764	2.6530612	52.959184
47	21	2.1428571	2.1341463	2.1428571	55.102041
48	24	2.4489796	2.4390244	2.4489796	57.551020
49	26	2.6530612	2.6422764	2.6530612	60.204082
50	26	2.6530612	2.6422764	2.6530612	62.857143
51	18	1.8367347	1.8292683	1.8367347	64.693878
52	18	1.8367347	1.8292683	1.8367347	66.530612
53	10	1.0204082	1.0162602	1.0204082	67.551020
54	17	1.7346939	1.7276423	1.7346939	69.285714
55	15	1.5306122	1.5243902	1.5306122	70.816327
56	21	2.1428571	2.1341463	2.1428571	72.959184
57	18	1.8367347	1.8292683	1.8367347	74.795918
58	13	1.3265306	1.3211382	1.3265306	76.122449
59	14	1.4285714	1.4227642	1.4285714	77.551020
60	17	1.7346939	1.7276423	1.7346939	79.285714
61	14	1.4285714	1.4227642	1.4285714	80.714286
62	19	1.9387755	1.9308943	1.9387755	82.653061
63	9	0.9183673	0.9146341	0.9183673	83.571429
64	10	1.0204082	1.0162602	1.0204082	84.591837
65	7	0.7142857	0.7113821	0.7142857	85.306122
66	11	1.1224490	1.1178862	1.1224490	86.428571
67	12	1.2244898	1.2195122	1.2244898	87.653061
68	7	0.7142857	0.7113821	0.7142857	88.367347
69	8	0.8163265	0.8130081	0.8163265	89.183673
70	11	1.1224490	1.1178862	1.1224490	90.306122
71	8	0.8163265	0.8130081	0.8163265	91.122449
72	8	0.8163265	0.8130081	0.8163265	91.938776
73	7	0.7142857	0.7113821	0.7142857	92.653061
74	11	1.1224490	1.1178862	1.1224490	93.775510
75	7	0.7142857	0.7113821	0.7142857	94.489796
76	5	0.5102041	0.5081301	0.5102041	95.000000
77	2	0.2040816	0.2032520	0.2040816	95.204082
78	8	0.8163265	0.8130081	0.8163265	96.020408
79	7	0.7142857	0.7113821	0.7142857	96.734694
80	2	0.2040816	0.2032520	0.2040816	96.938776
81	4	0.4081633	0.4065041	0.4081633	97.346939
82	4	0.4081633	0.4065041	0.4081633	97.755102
83	4	0.4081633	0.4065041	0.4081633	98.163265
84	3	0.3061224	0.3048780	0.3061224	98.469388
85	4	0.4081633	0.4065041	0.4081633	98.877551
86	3	0.3061224	0.3048780	0.3061224	99.183673
87	1	0.1020408	0.1016260	0.1020408	99.285714
88	2	0.2040816	0.2032520	0.2040816	99.489796
89	5	0.5102041	0.5081301	0.5102041	100.000000
#Total	980	100.0000000	99.5934959	100.0000000	NA
	4	NA	0.4065041	NA	NA

1.3.2 2.2. Variables Numéricas: Estadísticos Descriptivos

Para una variable continua como age, nos interesan medidas de tendencia central, dispersión y forma.

# Cálculo de descriptivos para la variable 'age'
descriptivos_edad <- datos %>%
  summarise(
    N_Validos = n(),
    Media = mean(age, na.rm = TRUE),
    Mediana = median(age, na.rm = TRUE),
    Desv_Estandar = sd(age, na.rm = TRUE),
    Minimo = min(age, na.rm = TRUE),
    Maximo = max(age, na.rm = TRUE),
    Rango = Maximo - Minimo,
    Asimetria = moments::skewness(age, na.rm = TRUE),
    Curtosis = moments::kurtosis(age, na.rm = TRUE) - 3 # Se resta 3 para obtener la curtosis "excesiva"
  )

# Mostramos la tabla de descriptivos
knitr::kable(descriptivos_edad, caption = "Estadísticos Descriptivos para Edad")

Estadísticos Descriptivos para Edad
N_Validos	Media	Mediana	Desv_Estandar	Minimo	Maximo	Rango	Asimetria	Curtosis
984	46.25408	45	16.72287	18	89	71	0.3882235	-0.5896465

Interpretación de Asimetría y Curtosis: - Asimetría: Un valor cercano a 0 indica simetría. Valores > 0 indican una cola larga a la derecha (sesgo positivo); valores < 0 indican una cola larga a la izquierda (sesgo negativo). - Curtosis (Excesiva): Mide qué tan “puntiaguda” es la distribución y cómo de pesadas son sus colas. Un valor cercano a 0 es similar a una normal (mesocúrtica). Un valor > 0 indica una forma más puntiaguda con colas pesadas (leptocúrtica). Un valor < 0 indica una forma más aplanada con colas ligeras (platicúrtica).

1.4 3. Comprobación de la Normalidad

Este es un supuesto clave para muchas pruebas paramétricas. Lo evaluaremos de dos formas: gráfica y estadística, replicando el menú Explorar de SPSS.

Hipótesis en las pruebas de normalidad: - Hipótesis Nula (H₀): Los datos provienen de una población con distribución normal. - Hipótesis Alternativa (Hₐ): Los datos NO provienen de una población con distribución normal.

Si el p-valor es < 0.05, rechazamos la H₀ y concluimos que no hay evidencia de normalidad.

1.4.1 3.1. Métodos Gráficos

Los gráficos son a menudo más informativos que las pruebas formales, especialmente con muestras grandes.

# Histograma con curva de densidad normal superpuesta
ggplot(datos, aes(x = age)) +
  geom_histogram(aes(y = ..density..), bins = 20, fill = "lightblue", color = "black") +
  stat_function(fun = dnorm, args = list(mean = mean(datos$age), sd = sd(datos$age)), color = "red", size = 1) +
  labs(title = "Histograma de Edad con Curva Normal", x = "Edad", y = "Densidad") +
  theme_minimal()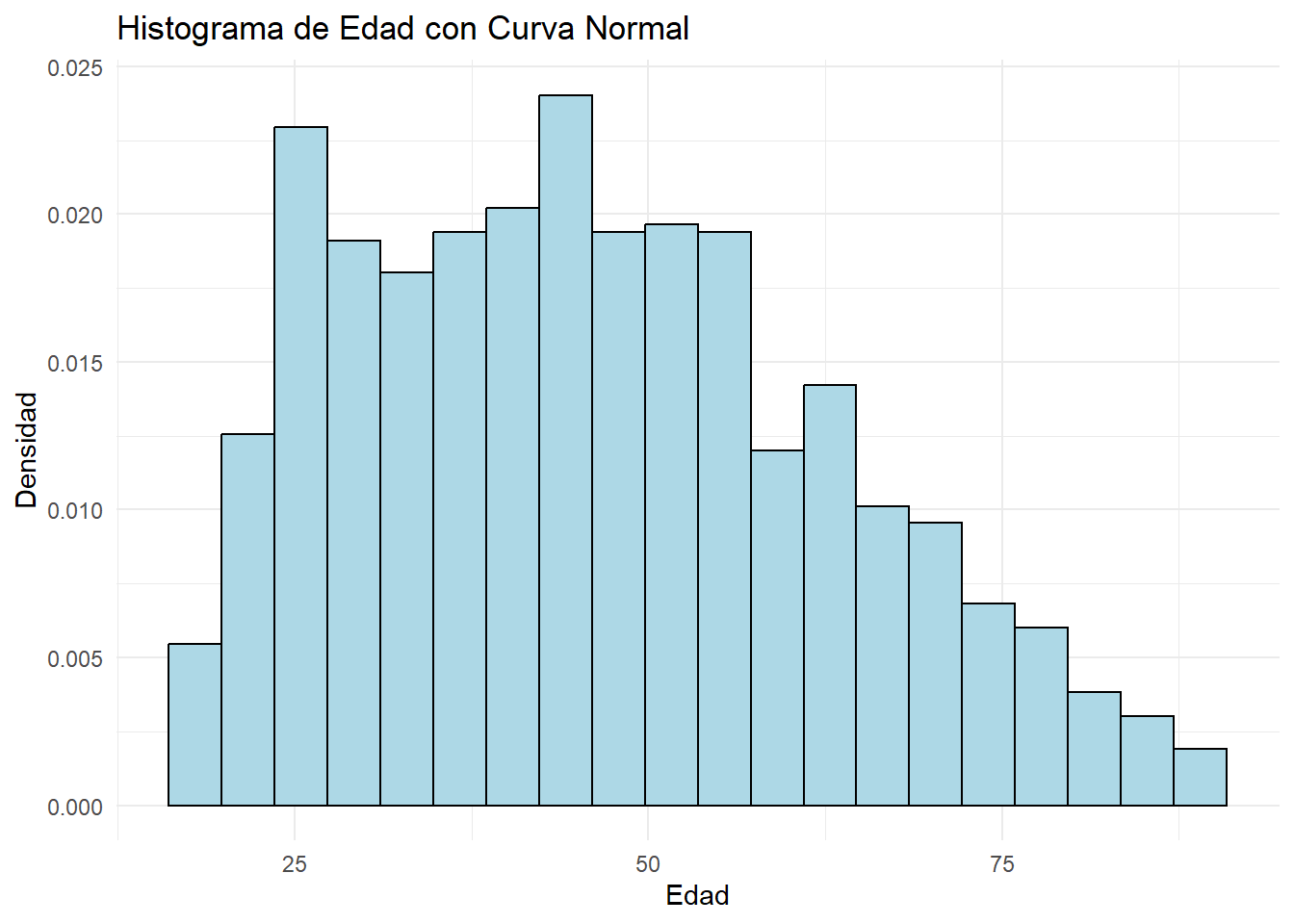

# Gráfico Q-Q (Quantile-Quantile)
ggplot(datos, aes(sample = age)) +
  stat_qq() +
  stat_qq_line(color = "blue") +
  labs(title = "Gráfico Q-Q para la Variable Edad", x = "Cuantiles Teóricos (Normal)", y = "Cuantiles de la Muestra") +
  theme_minimal()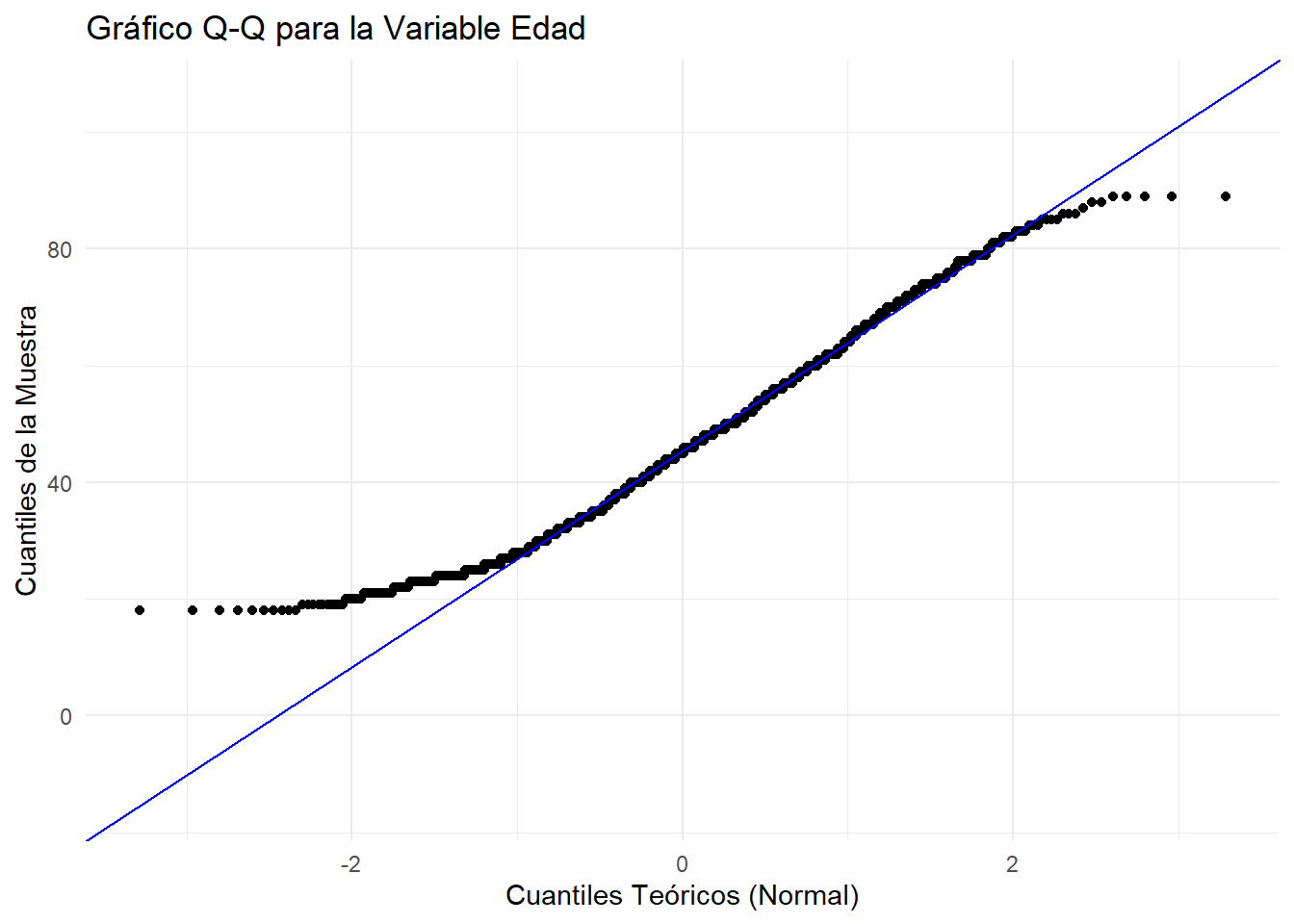

Interpretación Gráfica: - Histograma: Comparamos visualmente la forma de las barras con la curva normal teórica (roja). - Gráfico Q-Q: Si los puntos se ajustan estrechamente a la línea diagonal, es una fuerte indicación de normalidad. Desviaciones sistemáticas (en forma de “S” o “banana”) sugieren no-normalidad.

1.4.2 3.2. Pruebas Estadísticas

1.4.2.1 a) Prueba de Shapiro-Wilk

Es la prueba más potente y recomendada para la normalidad, especialmente con muestras de menos de 2000-5000 casos.

# Realizamos la prueba de Shapiro-Wilk
shapiro_test_resultado <- shapiro.test(datos$age)
print(shapiro_test_resultado)


    Shapiro-Wilk normality test

data:  datos$age
W = 0.97233, p-value = 1.033e-12

Interpretación: Observamos el p-value. Si es menor a 0.05, rechazamos la normalidad.

1.4.2.2 b) Prueba de Kolmogorov-Smirnov con corrección de Lilliefors

Es una alternativa, aunque generalmente menos potente que Shapiro-Wilk para probar la normalidad.

# Realizamos la prueba de K-S con corrección de Lilliefors
lillie_test_resultado <- lillie.test(datos$age)
print(lillie_test_resultado)


    Lilliefors (Kolmogorov-Smirnov) normality test

data:  datos$age
D = 0.065845, p-value = 8.869e-11

Interpretación: La lógica es la misma. Si el p-value es menor a 0.05, rechazamos la normalidad.

1.5 4. Comprobación de la Homoscedasticidad

Esta es la prueba formal para la igualdad de varianzas. Al igual que en la documentación usamos otro fichero, hatco.sav.

La homoscedasticidad, o igualdad de varianzas, es un supuesto clave para pruebas que comparan grupos (como el test t para muestras independientes o el ANOVA). Significa que la dispersión de la variable continua es la misma en todos los grupos.

Hipótesis en el Test de Levene: - Hipótesis Nula (H₀): Las varianzas de los grupos son iguales (hay homoscedasticidad). - Hipótesis Alternativa (Hₐ): Al menos una varianza es diferente (hay heteroscedasticidad).

Si el p-valor es < 0.05, rechazamos la H₀ y concluimos que las varianzas no son homogéneas.

1.5.1 Ejemplo: ¿La dispersión de la valoración en la rapidez del servicio y/o en el nivel de servicio es la misma para las empresas grandes y pequeñas?

1.5.2 4.1. Método Gráfico

Los diagramas de caja (boxplots) son la mejor herramienta visual para comparar la dispersión entre grupos.

datos <- read_sav('data/hatco.sav')

# Diagramas de caja
ggplot(datos, aes(x = X8, y = X1 , fill = X8)) +
  geom_boxplot() +
  labs(
    title = "Dispersión de Valoración por Tamaño de empresa",
    x = "Tamaño empresa",
    y = "Valoración de la rapidez de servicio"
  ) +
  theme_minimal() +
  theme(legend.position = "none")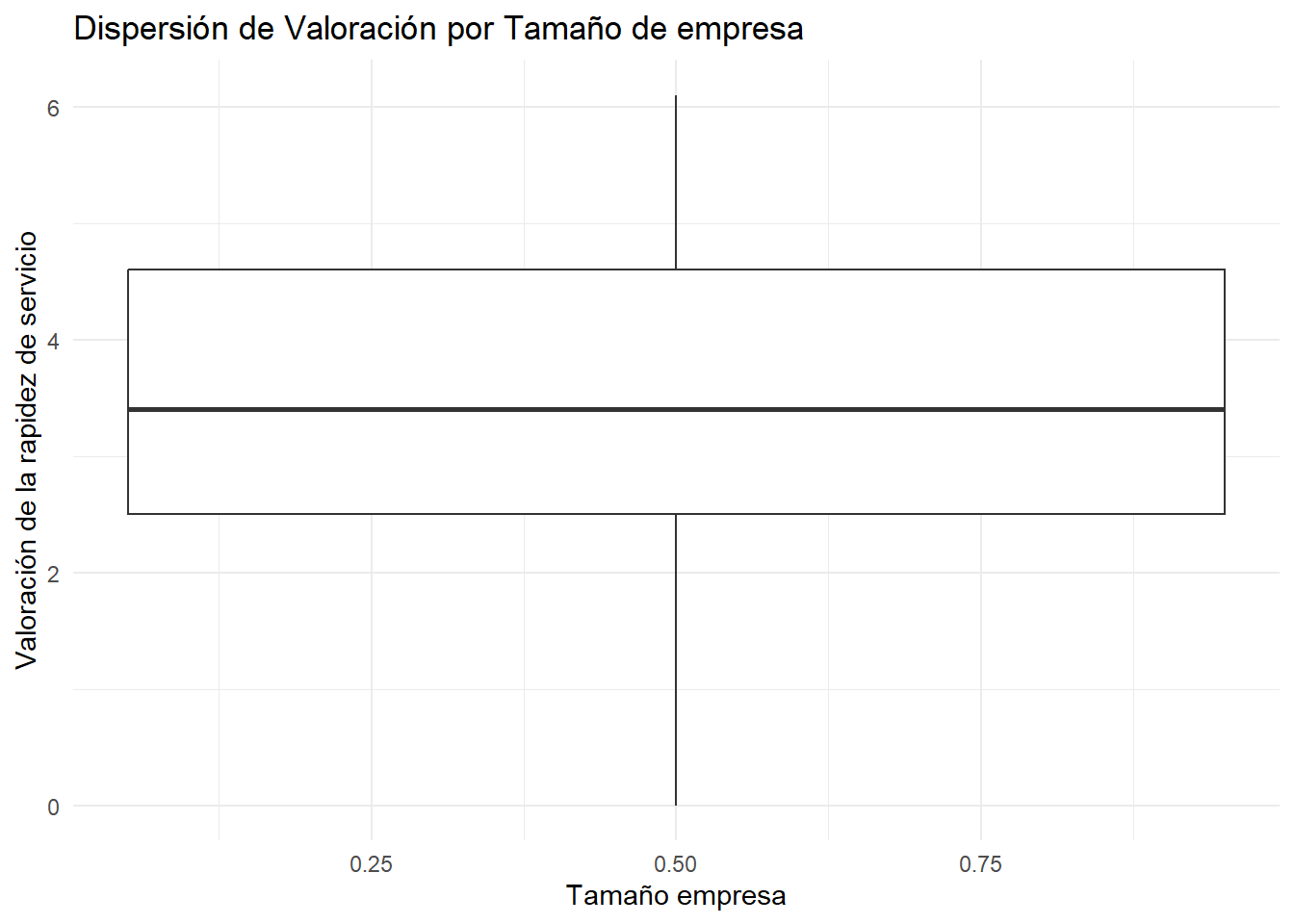

ggplot(datos, aes(x = X8, y = X5, fill = X8)) +
  geom_boxplot() +
  labs(
    title = "Dispersión de Valoración por Tamaño de empresa",
    x = "Tamaño empresa",
    y = "Valoración del nivel de servicio"
  ) +
  theme_minimal() +
  theme(legend.position = "none")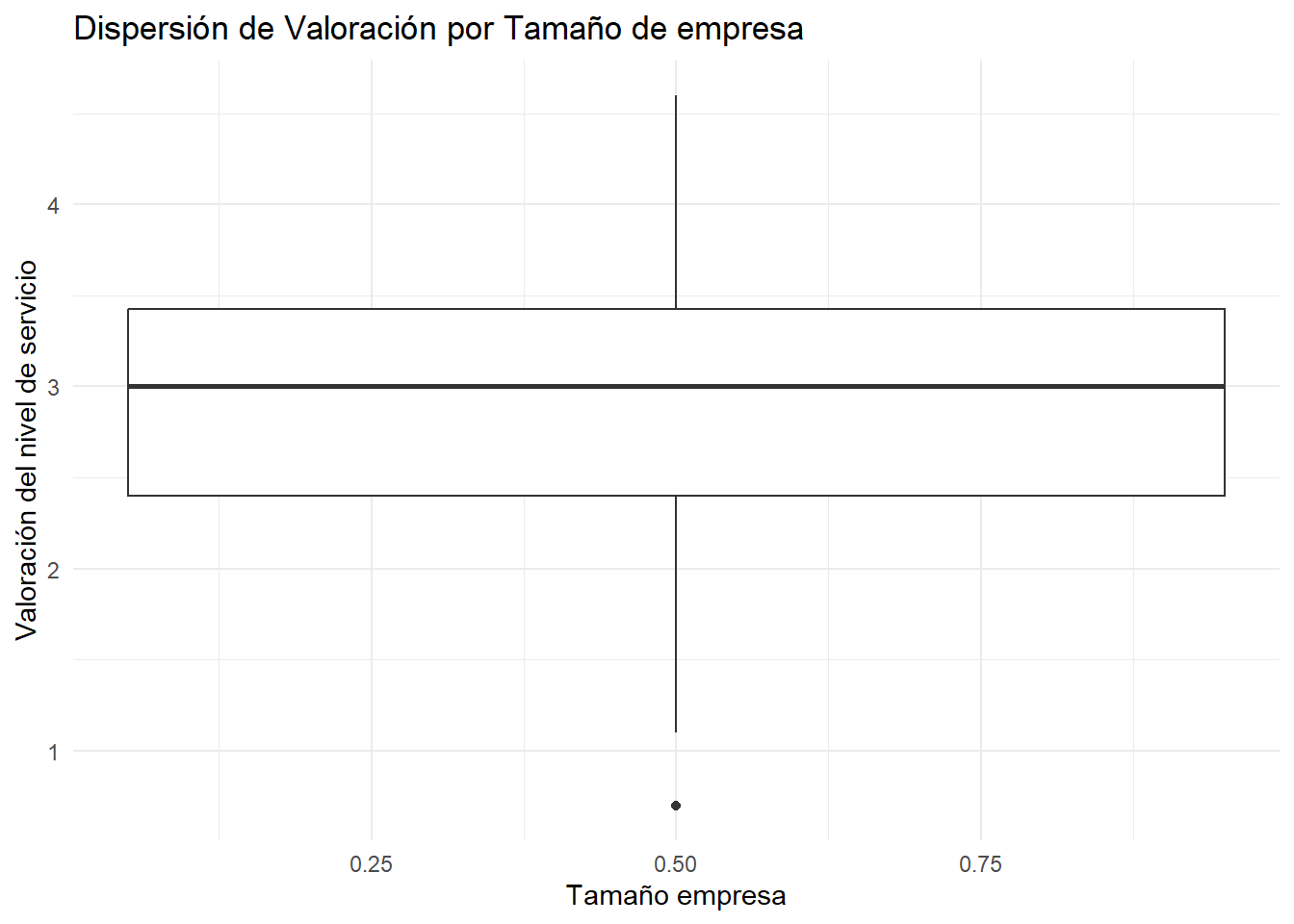

Interpretación Gráfica: Comparamos la altura de las cajas (que representa el Rango Intercuartílico). Si las cajas tienen alturas muy diferentes, podría ser un indicio de heteroscedasticidad.

1.5.3 4.2. Prueba Estadística: Test de Levene

# Realizamos el Test de Levene

levene_test_resultado1 <- leveneTest(X1 ~ factor(X8), data = datos)
levene_test_resultado2 <- leveneTest(X5 ~ factor(X8), data = datos)

print(levene_test_resultado1)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1   0.993 0.3215
      98

print(levene_test_resultado2)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value  Pr(>F)  
group  1  6.7411 0.01087 *
      98                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretación: Observamos el p-valor (Pr(>F)). Si es menor a 0.05, concluimos que las varianzas son significativamente diferentes. Si es mayor a 0.05, no tenemos evidencia para rechazar la H₀ y podemos asumir homoscedasticidad.

1.6 Conclusión

Hemos completado el primer paso (“Punto 0”) de nuestro viaje en el análisis de datos. Ahora sabemos cómo cargar datos, obtener descriptivos y, lo más importante, cómo validar los supuestos de normalidad y homoscedasticidad en R. Esta base nos permitirá elegir con confianza entre pruebas paramétricas y no paramétricas en las próximas sesiones. ```