# Paquetes para manipulación, visualización y lectura de datos
library(tidyverse)
library(haven)
# Paquetes específicos para el Análisis de Correspondencias
# install.packages(c("ca", "FactoMineR", "factoextra"))
library(ca)
library(FactoMineR)
library(factoextra)
library(gplots)4 Análisis de correspondencias simple (ANACO)
Creando Mapas Perceptuales en R
4.1 Introducción
El Análisis de Correspondencias (ANACO o CA, por sus siglas en inglés) es una técnica multivariante de interdependencia que nos permite visualizar las relaciones entre las categorías de dos variables nominales. Su principal resultado es un mapa perceptual, un gráfico de dispersión que posiciona las categorías de las filas y columnas de una tabla de contingencia en un espacio de pocas dimensiones (generalmente dos).
En investigación de mercados, es una herramienta insustituible para: - Posicionamiento de marca: Entender cómo los consumidores perciben diferentes marcas en función de una serie de atributos. - Segmentación de mercados: Visualizar las asociaciones entre diferentes segmentos de clientes y sus preferencias o comportamientos. - Análisis de imagen: Evaluar la relación entre una empresa y los atributos con los que se la asocia.
En esta sesión, aprenderemos a realizar un ANACO desde cero, interpretando cada uno de sus componentes para extraer insights valiosos.
4.1.1 Carga de Paquetes
Cargamos todos los paquetes que necesitaremos. ca es el paquete clásico de Michael Greenacre, uno de los pioneros de esta técnica. FactoMineR y factoextra forman un ecosistema muy potente para el análisis y, sobre todo, la visualización de resultados multivariantes.
4.2 1. El Caso de Estudio: HATCO
Contexto: HATCO, una empresa de maquinaria industrial, quiere entender su posición competitiva. Ha realizado un estudio donde se ha preguntado a clientes qué atributos (X1 a X8) asocian con HATCO y sus 9 principales competidores (A a I). El resultado es una tabla de contingencia que muestra la frecuencia con la que cada empresa ha sido asociada con cada atributo.
Objetivo: Crear un mapa perceptual para visualizar qué empresas compiten más directamente entre sí y qué atributos definen el posicionamiento de cada una.
4.2.1 Preparación de los Datos
En muchos escenarios reales, no partimos de datos brutos, sino de una tabla ya agregada. Nuestro primer paso es cargar esta tabla en R y prepararla para el análisis.
# Leemos la tabla de contingencia desde un archivo CSV
# Esta tabla contiene los atributos en las filas y las empresas en las columnas
tabla_hatco <- read_csv("data/tabla.hatco.anacor.csv")
# El paquete `ca` requiere que los nombres de las filas (atributos) no sean una columna,
# sino los "rownames" de la tabla. Hacemos esa transformación.
tabla_hatco_ca <- tabla_hatco %>%
column_to_rownames(var = "atributo") # La primera columna se convierte en nombres de fila
# Echamos un vistazo a la tabla final
knitr::kable(tabla_hatco_ca, caption = "Tabla de Contingencia: Atributos vs. Empresas")| hatco | a | b | c | d | e | f | g | h | i | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 16 | 13 | 8 | 13 | 9 | 17 | 15 | 16 | 6 | 12 |
| x2 | 14 | 14 | 10 | 11 | 11 | 14 | 12 | 13 | 10 | 14 |
| x3 | 6 | 6 | 14 | 10 | 11 | 8 | 7 | 4 | 14 | 4 |
| x4 | 15 | 18 | 9 | 2 | 3 | 15 | 16 | 7 | 8 | 8 |
| x5 | 15 | 14 | 6 | 4 | 4 | 15 | 14 | 13 | 7 | 13 |
| x6 | 7 | 18 | 13 | 4 | 9 | 16 | 14 | 5 | 4 | 16 |
| x7 | 4 | 3 | 1 | 13 | 9 | 6 | 3 | 18 | 2 | 10 |
| x8 | 15 | 16 | 15 | 11 | 11 | 14 | 16 | 12 | 14 | 14 |
4.3 2. ¿Existe una Relación para Analizar? La Prueba de Chi-cuadrado
Antes de sumergirnos en el ANACO, debemos responder una pregunta fundamental: ¿son las variables (atributos y empresas) independientes o, por el contrario, existe una asociación significativa entre ellas? Si fueran independientes, no tendría sentido buscar un patrón de asociación.
La Prueba de Chi-cuadrado (χ²) de independencia es el test adecuado para esto.
- Hipótesis Nula (H₀): No hay asociación entre los atributos y las empresas (son independientes).
- Hipótesis Alternativa (Hₐ): Existe una asociación entre los atributos y las empresas.
# Realizamos la prueba de Chi-cuadrado sobre nuestra tabla
test_chi <- chisq.test(tabla_hatco_ca)
print(round(test_chi$expected,0)) hatco a b c d e f g h i
x1 14 15 11 10 10 15 14 13 10 13
x2 13 15 11 10 10 15 14 13 9 13
x3 9 10 8 7 7 10 10 9 6 9
x4 11 12 9 8 8 12 12 10 8 11
x5 11 13 9 8 8 13 12 11 8 11
x6 11 13 9 8 8 13 12 11 8 11
x7 7 8 6 6 5 9 8 7 5 7
x8 15 17 12 11 11 17 16 14 11 15print(round(test_chi$residuals,2)) hatco a b c d e f g h i
x1 0.68 -0.51 -0.95 0.95 -0.27 0.40 0.20 0.86 -1.15 -0.37
x2 0.19 -0.19 -0.30 0.37 0.42 -0.30 -0.54 0.08 0.20 0.23
x3 -1.02 -1.28 2.37 1.27 1.71 -0.73 -0.83 -1.59 2.99 -1.66
x4 1.24 1.69 -0.01 -2.14 -1.76 0.72 1.32 -1.07 0.10 -0.85
x5 1.08 0.40 -1.10 -1.52 -1.48 0.57 0.59 0.65 -0.36 0.53
x6 -1.32 1.49 1.15 -1.54 0.23 0.81 0.55 -1.80 -1.44 1.39
x7 -1.27 -1.83 -2.08 3.19 1.53 -0.86 -1.73 4.07 -1.42 0.97
x8 0.02 -0.13 0.76 -0.01 0.04 -0.73 0.07 -0.60 1.07 -0.20print(round(test_chi$stdres,2)) hatco a b c d e f g h i
x1 0.78 -0.59 -1.07 1.08 -0.30 0.46 0.23 0.98 -1.29 -0.43
x2 0.22 -0.22 -0.34 0.42 0.48 -0.35 -0.62 0.09 0.22 0.27
x3 -1.14 -1.44 2.62 1.39 1.87 -0.83 -0.93 -1.77 3.28 -1.85
x4 1.39 1.92 -0.01 -2.37 -1.95 0.82 1.50 -1.20 0.11 -0.96
x5 1.22 0.45 -1.23 -1.69 -1.65 0.65 0.67 0.73 -0.40 0.60
x6 -1.49 1.69 1.29 -1.71 0.25 0.92 0.63 -2.03 -1.60 1.57
x7 -1.40 -2.04 -2.27 3.47 1.66 -0.96 -1.92 4.48 -1.55 1.07
x8 0.02 -0.15 0.87 -0.01 0.05 -0.86 0.08 -0.69 1.21 -0.23print(test_chi)
Pearson's Chi-squared test
data: tabla_hatco_ca
X-squared = 122.6, df = 63, p-value = 1.033e-05Interpretación: El p-valor es extremadamente bajo (p-value < 2.2e-16), mucho menor que el umbral de 0.05. Por lo tanto, rechazamos la hipótesis nula. Concluimos con gran confianza que existe una relación significativa entre las empresas y los atributos con los que se las asocia. ¡Tiene sentido proceder con el Análisis de Correspondencias!
4.4 3. Realización del Análisis de Correspondencias
El análisis de correspondencias no es exigente con las propiedades estadísticas de los datos. Como ya indicamos, utiliza variables no métricas en su forma más simple (tabla de contingencia), pero sin embargo hay que ser cuidadoso respecto al sentido del análisis en función de la representación de los datos.
En nuestro ejemplo pensemos que …
- Los poseedores de los atributos son comparables respecto a esos atributos.
- Confirmar que las empresas A,B, …, I son efectivamente competidoras de HATCO.
- Que basan su diferenciación en los atributos X1 a X8.
- El listado de atributos debe ser exhaustivo y no dejamos ninguno relevante para la caracterización de las empresas.
Comenzamos por ver la relevancia de la tabla, validar si realmente hay un cierto nivel de dependencia entre las categorías de fila y las categorías de columna. Para ello utilizamos la prueba Chi2.
4.5 Nuestro ejemplo
HATCO quiere identificar a sus principales competidores:
- Quiere hacerlo en función de su posición respecto a las principales variables de competencia:
- X1 Rapidez del servicio
- X2 Nivel de precios
- X3 Flexibilidad de precios
- X4 Imagen del fabricante
- X5 Calidad del servicio
- X6 Imagen de los vendedores
- X7 Calidad del producto
- X8 Tamaño de la empresa
- La medida que se utiliza es la asociación de la característica con el competidor. Para ello se ha utilizado una transformación de la medición original a una caracterización (0/1).
- En nuestro ejemplo: en la tabla de contingencia, una frecuencia de 1 implica que ese competidor se ha señalado como “que dispone de la característica competitiva” en la característica o atributo de fila.
4.6 Análisis de correspondencias simple (Michael Greenacre)
Calculamos utilizando el paquete ca de Michael Greenacre. Sus resultados son semejantes a SPSS pero el mapa sale invertido en cuadrantes, lo que no implica distinta interpretación.
4.6.1 Resumen de resultados
Obtenemos los resultados más característicos con la función ca(). Almacenamos el objeto para ir mostrando después más completos sus resultados
res <- ca(tabla_hatco_ca)
res
Principal inertias (eigenvalues):
1 2 3 4 5 6 7
Value 0.076541 0.047813 0.015291 0.002658 0.000806 0.000576 0.000381
Percentage 53.13% 33.19% 10.61% 1.84% 0.56% 0.4% 0.26%
Rows:
x1 x2 x3 x4 x5 x6 x7
Mass 0.146886 0.144536 0.098707 0.118684 0.123384 0.124559 0.081081
ChiDist 0.199723 0.088497 0.580707 0.400294 0.285309 0.386846 0.808039
Inertia 0.005859 0.001132 0.033286 0.019017 0.010044 0.018640 0.052940
Dim. 1 0.388333 0.219066 0.083693 -1.285544 -0.383784 -0.836930 2.863462
Dim. 2 0.524538 -0.097621 -2.641197 0.610370 1.073949 0.211061 0.636902
x8
Mass 0.162162
ChiDist 0.139329
Inertia 0.003148
Dim. 1 -0.153942
Dim. 2 -0.524856
Columns:
hatco a b c d e f
Mass 0.108108 0.119859 0.089307 0.079906 0.078731 0.123384 0.113984
ChiDist 0.287008 0.321688 0.430028 0.569393 0.402272 0.184239 0.257577
Inertia 0.008905 0.012403 0.016515 0.025906 0.012740 0.004188 0.007562
Dim. 1 -0.470333 -1.021735 -0.843200 1.933384 0.969935 -0.449822 -0.838114
Dim. 2 0.626124 0.580139 -1.583295 -0.793574 -1.189113 0.502451 0.446827
g h i
Mass 0.103408 0.076381 0.106933
ChiDist 0.532696 0.491456 0.274442
Inertia 0.029344 0.018448 0.008054
Dim. 1 1.680687 -0.392286 0.233423
Dim. 2 1.092070 -1.944341 0.784252Para poder representar gráficamente los datos de la tabla, se debe reducir la dimensionalidad, puesto que solo vamos a ser capaces de ver los datos en mapas de dos dimensiones, o como mucho en tres. El mapa explica en sus dos primeras dimensiones el 86,3% de la información original (suma de las dos primeras dimensiones).
Podemos luego combinar para otras dimensiones, 1-3, 2-5 pero es muy poco habitual, dado que la pérdida de información (y por tanto la dificultad de explicación) es muy alta.
Analicemos ahora poco a poco los elementos que componen el análisis.
Algunos datos relevantes son:
- Llamamos perfil al vector formado por los elementos de columna y/o fila.
- Llamamos perfil medio al perfil total de columna y/o al perfil total de columna.
Otra forma de verlo:
* Las coordenadas en el mapa se calculan utilizando algunos conceptos típicos en el análisis multivariante:
* La inercia total, o medida de dispersión entre los perfiles y el perfil promedio, es un indicador de la dispersión o falta de correspondencia entre un punto fila y/o columna. Se calcula como el valor de Chi-cuadrado cociente con el total de casos.- La hipótesis nula es una transformación de la estándar, el perfil medio sería la homogeneidad de los perfiles (Ho en Chi-cuadrado es la independencia).
- Homogeneidad = Independencia.
- Heterogeneidad = Dependencia.
4.6.1.0.1 Valor singular
res[["sv"]] #extraemos el elemento llamado sv[1] 0.27666126 0.21866273 0.12365880 0.05155155 0.02838433 0.02400166 0.019514414.6.1.1 Análisis de las filas
4.6.1.1.1 Nombre de las filas (atributos)
res[["rownames"]][1] "x1" "x2" "x3" "x4" "x5" "x6" "x7" "x8"4.6.1.1.2 Masa de las filas (perfil)
Perfiles de las filas, son los porcentajes horizontales, aunque no se llaman así porque en muchos casos las columnas y/o filas de la tabla no son realmente categorías de una misma variable (frecuencias relativas). Llamados masa, es el cálculo de los porcentajes marginales (sin contar con la otra variable), denominado en algunos casos el perfil medio o también centroide o baricentro. Es decir el peso del atributo o de la empresa en el total marginal.
res[["rowmass"]][1] 0.14688602 0.14453584 0.09870740 0.11868390 0.12338425 0.12455934 0.08108108
[8] 0.162162164.6.1.1.3 Distancia de las filas
La representación de los datos de la tabla en el mapa se hace atendiendo al cálculo de distancias. El concepto de distancia, en este caso la distancia Chi-cuadrado o cálculo de la distancia euclídea entre los vectores fila y su masa de fila.
res[["rowdist"]][1] 0.19972301 0.08849696 0.58070663 0.40029405 0.28530854 0.38684579 0.80803871
[8] 0.139329074.6.1.1.4 Inercia de las filas
La inercia de cada perfil se calcula como producto de la masa por el cuadrado de la distancia chi-cuadrado de ese perfil al promedio. La inercia mide lo lejos que se hallan los perfiles fila o columna de su perfil medio.
res[["rowinertia"]][1] 0.005859178 0.001131963 0.033286129 0.019017354 0.010043597 0.018640264
[7] 0.052939991 0.0031479884.6.1.1.5 Coordenadas de las filas
Punto de ubicación en el mapa de cada punto fila.
res[["rowcoord"]] Dim1 Dim2 Dim3 Dim4 Dim5 Dim6
x1 0.38833337 0.52453784 -0.48064888 2.0327480 -0.7993536 -0.3021486
x2 0.21906639 -0.09762105 -0.05138317 -0.4795627 -1.3748826 0.7323587
x3 0.08369285 -2.64119673 -0.34019450 0.2493870 0.6347806 -1.2085960
x4 -1.28554439 0.61037038 -0.89764463 0.4026826 1.7762794 0.8684848
x5 -0.38378371 1.07394894 -0.73674199 -1.3240795 -0.2697071 -1.8311119
x6 -0.83693026 0.21106121 2.47591880 0.1896399 0.1476687 -0.2958822
x7 2.86346220 0.63690241 0.48320469 -0.4465221 1.4975360 0.2144778
x8 -0.15394237 -0.52485592 -0.23761538 -0.7752912 -0.3939105 1.2342381
Dim7
x1 0.53731697
x2 -1.78938738
x3 -0.32626826
x4 -0.72333444
x5 0.28708482
x6 0.08839279
x7 -0.08239776
x8 1.591052494.6.1.2 Análisis de las columnas
4.6.1.2.1 Nombre de las columnas (las marcas)
res[["colnames"]] [1] "hatco" "a" "b" "c" "d" "e" "f" "g" "h"
[10] "i" 4.6.1.2.2 Masa de las columnas (perfil)
Perfiles de las columnas, son los porcentajes verticales, aunque no se llaman así porque en muchos casos las columnas y/o filas de la tabla no son realmente categorías de una misma variable (frecuencias relativas). Llamados masa, es el cálculo de los porcentajes marginales (sin contar con la otra variable), denominado en algunos casos el perfil medio o también centroide o baricentro. Es decir el peso del atributo o de la empresa en el total marginal.
res[["colmass"]] [1] 0.10810811 0.11985899 0.08930670 0.07990599 0.07873090 0.12338425
[7] 0.11398355 0.10340776 0.07638073 0.106933024.6.1.2.3 Distancia de las columnas
La representación de los datos de la tabla en el mapa se hace atendiendo al cálculo de distancias. El concepto de distancia, en este caso la distancia Chi-cuadrado o cálculo de la distancia euclídea entre los vectores columna y su masa de columna.
res[["coldist"]] [1] 0.2870082 0.3216884 0.4300280 0.5693934 0.4022721 0.1842392 0.2575766
[8] 0.5326961 0.4914556 0.27444164.6.1.2.4 Inercia de las columnas
La inercia de cada perfil se calcula como producto de la masa por el cuadrado de la distancia chi-cuadrado de ese perfil al promedio. La inercia mide lo lejos que se hallan los perfiles fila o columna de su perfil medio.
res[["colinertia"]] [1] 0.008905264 0.012403421 0.016514959 0.025906232 0.012740460 0.004188165
[7] 0.007562317 0.029343514 0.018448129 0.0080540004.6.1.2.5 Coordenadas de las columnas
Punto de ubicación en el mapa de cada punto columna.
res[["colcoord"]] Dim1 Dim2 Dim3 Dim4 Dim5 Dim6
hatco -0.4703327 0.6261240 -1.6935356 0.29465670 -1.7292066 0.4655331
a -1.0217346 0.5801388 0.5338336 -0.07823246 1.1100906 1.6894406
b -0.8432000 -1.5832948 0.7964316 0.26209544 0.2874627 -0.1659282
c 1.9333842 -0.7935744 -0.1648613 1.59150233 -0.5015929 1.0023065
d 0.9699347 -1.1891134 1.1762320 0.24157388 -0.3215290 0.1038722
e -0.4498224 0.5024514 0.2356379 1.01941582 0.2256877 -2.0473172
f -0.8381141 0.4468266 -0.2145714 0.65967745 0.3110986 0.1309981
g 1.6806871 1.0920696 -0.6758338 -0.77145803 1.5096436 -0.3224750
h -0.3922857 -1.9443407 -1.6117961 -1.83337906 0.3985224 -0.4838085
i 0.2334232 0.7842522 1.4674729 -1.62005491 -1.4611537 -0.1711086
Dim7
hatco -0.4460250
a -1.1173385
b 1.3363279
c 0.3955033
d -1.4550986
e -0.9157056
f 1.6885279
g 0.4368324
h -0.4346288
i 0.50781094.6.2 Representación gráfica: los mapas de puntos
plot(res)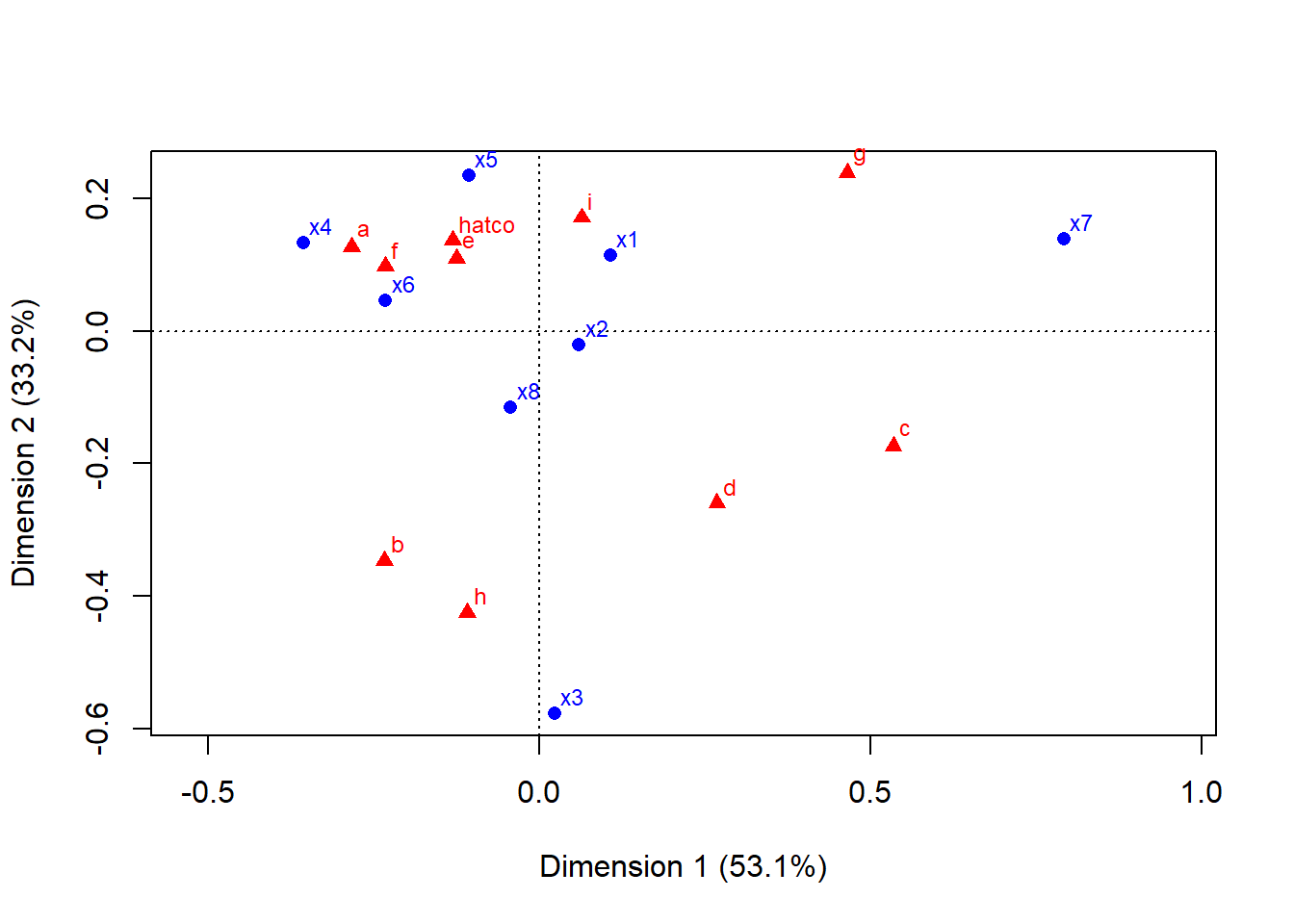
plot(res, lines=TRUE)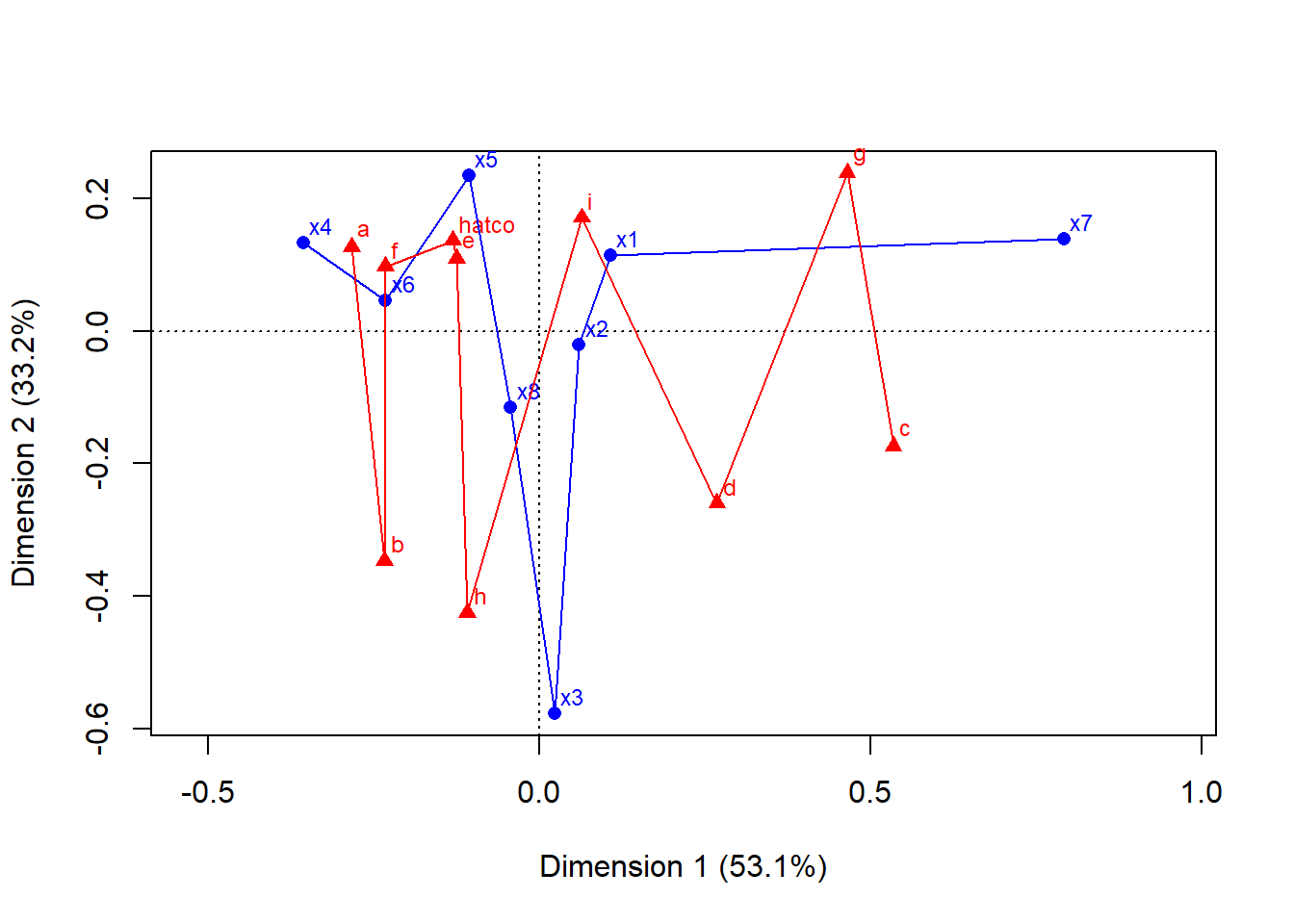
plot(res, arrows=c(TRUE, TRUE))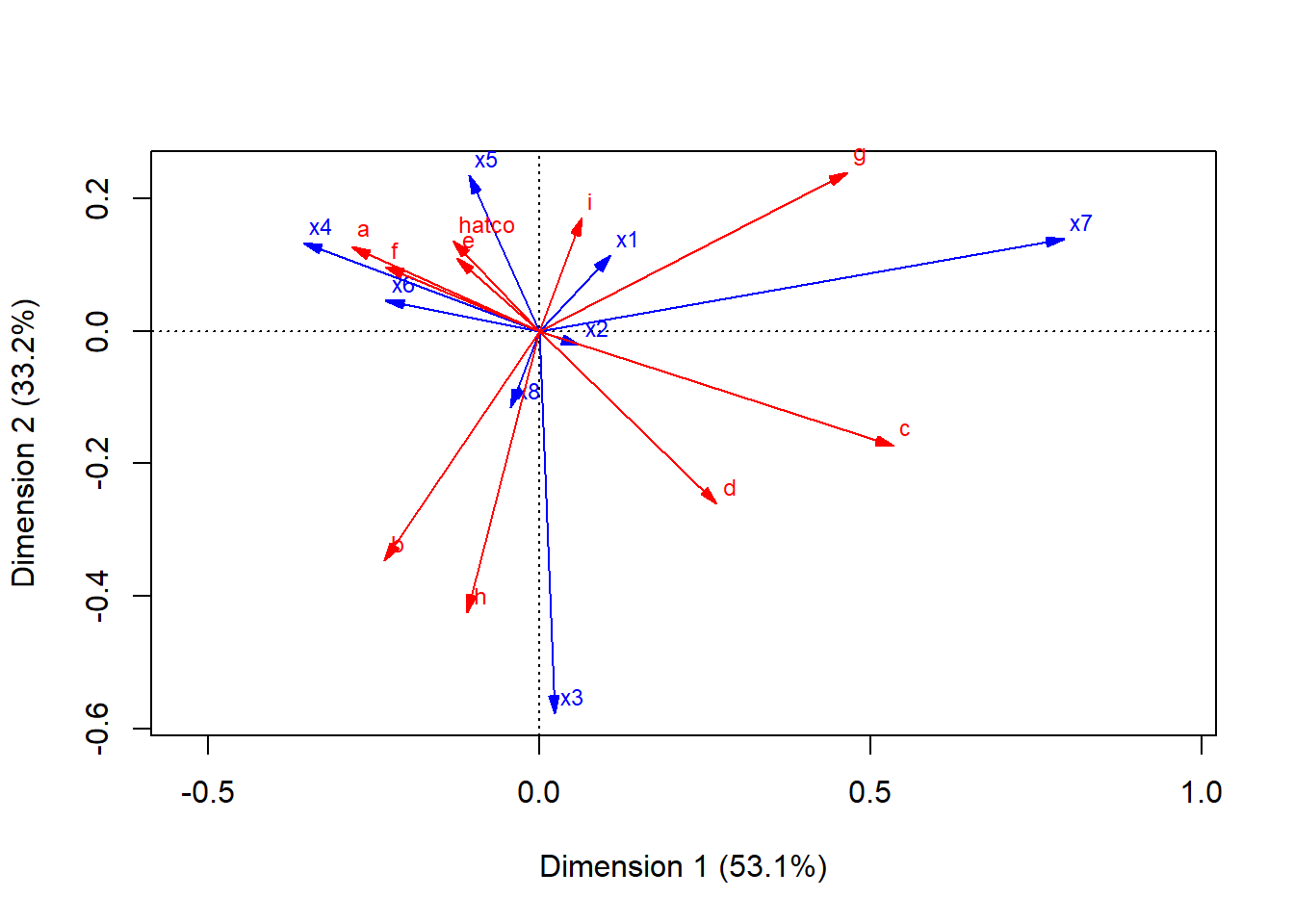
4.7 Análisis de correspondencias (CA de FactoMineR)
Ahora hacemos el cálculo con el algoritmo CA (nótese diferencia por mayúsculas) del paquete FactoMineR. Generamos una salida de tabla en modo gráfico, donde visualmente el diámetro de la circunferencia es mayor cuanto mayor sea el valor de la celda
dtmatrix <- as.matrix(tabla_hatco_ca)
dttable <- as.table(dtmatrix)
balloonplot(t(dttable),main = "Empresa * Atributo",xlab = "Empresa",ylab = "Atributo",label = TRUE,show.margins = TRUE)
El paquete FactoMineR, que ofrece una salida muy completa y se integra a la perfección con factoextra para las visualizaciones.
# Ejecutamos el análisis con la función CA()
res_ca <- CA(tabla_hatco_ca, graph = FALSE)
# Obtenemos un resumen de los resultados
summary(res_ca)
Call:
CA(X = tabla_hatco_ca, graph = FALSE)
The chi square of independence between the two variables is equal to 122.6006 (p-value = 1.033292e-05 ).
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
Variance 0.077 0.048 0.015 0.003 0.001 0.001 0.000
% of var. 53.129 33.188 10.614 1.845 0.559 0.400 0.264
Cumulative % of var. 53.129 86.318 96.932 98.777 99.336 99.736 100.000
Rows
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr
x1 | 5.859 | 0.107 2.215 0.289 | -0.115 4.041 0.330 | 0.059 3.393
x2 | 1.132 | 0.061 0.694 0.469 | 0.021 0.138 0.058 | 0.006 0.038
x3 | 33.286 | 0.023 0.069 0.002 | 0.578 68.857 0.989 | 0.042 1.142
x4 | 19.017 | -0.356 19.614 0.789 | -0.133 4.422 0.111 | 0.111 9.563
x5 | 10.044 | -0.106 1.817 0.138 | -0.235 14.231 0.677 | 0.091 6.697
x6 | 18.640 | -0.232 8.725 0.358 | -0.046 0.555 0.014 | -0.306 76.357
x7 | 52.940 | 0.792 66.482 0.961 | -0.139 3.289 0.030 | -0.060 1.893
x8 | 3.148 | -0.043 0.384 0.093 | 0.115 4.467 0.678 | 0.029 0.916
cos2
x1 0.089 |
x2 0.005 |
x3 0.005 |
x4 0.077 |
x5 0.102 |
x6 0.626 |
x7 0.005 |
x8 0.044 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr
hatco | 8.905 | -0.130 2.391 0.206 | -0.137 4.238 0.228 | 0.209 31.006
a | 12.403 | -0.283 12.513 0.772 | -0.127 4.034 0.156 | -0.066 3.416
b | 16.515 | -0.233 6.350 0.294 | 0.346 22.388 0.648 | -0.098 5.665
c | 25.906 | 0.535 29.869 0.882 | 0.174 5.032 0.093 | 0.020 0.217
d | 12.740 | 0.268 7.407 0.445 | 0.260 11.132 0.418 | -0.145 10.893
e | 4.188 | -0.124 2.497 0.456 | -0.110 3.115 0.356 | -0.029 0.685
f | 7.562 | -0.232 8.007 0.810 | -0.098 2.276 0.144 | 0.027 0.525
g | 29.344 | 0.465 29.210 0.762 | -0.239 12.333 0.201 | 0.084 4.723
h | 18.448 | -0.109 1.175 0.049 | 0.425 28.875 0.748 | 0.199 19.843
i | 8.054 | 0.065 0.583 0.055 | -0.171 6.577 0.390 | -0.181 23.028
cos2
hatco 0.532 |
a 0.042 |
b 0.052 |
c 0.001 |
d 0.131 |
e 0.025 |
f 0.011 |
g 0.025 |
h 0.164 |
i 0.437 |4.7.1 ¿Cuántas Dimensiones Necesitamos? La Inercia
El ANACO descompone la “inercia total” de la tabla (una medida de la dispersión, relacionada con el Chi-cuadrado) en varias dimensiones ortogonales. El gráfico de sedimentación (scree plot) nos ayuda a decidir cuántas dimensiones retener.
# Visualizamos el porcentaje de inercia (varianza) explicado por cada dimensión
fviz_eig(res_ca, addlabels = TRUE, ylim = c(0, 60))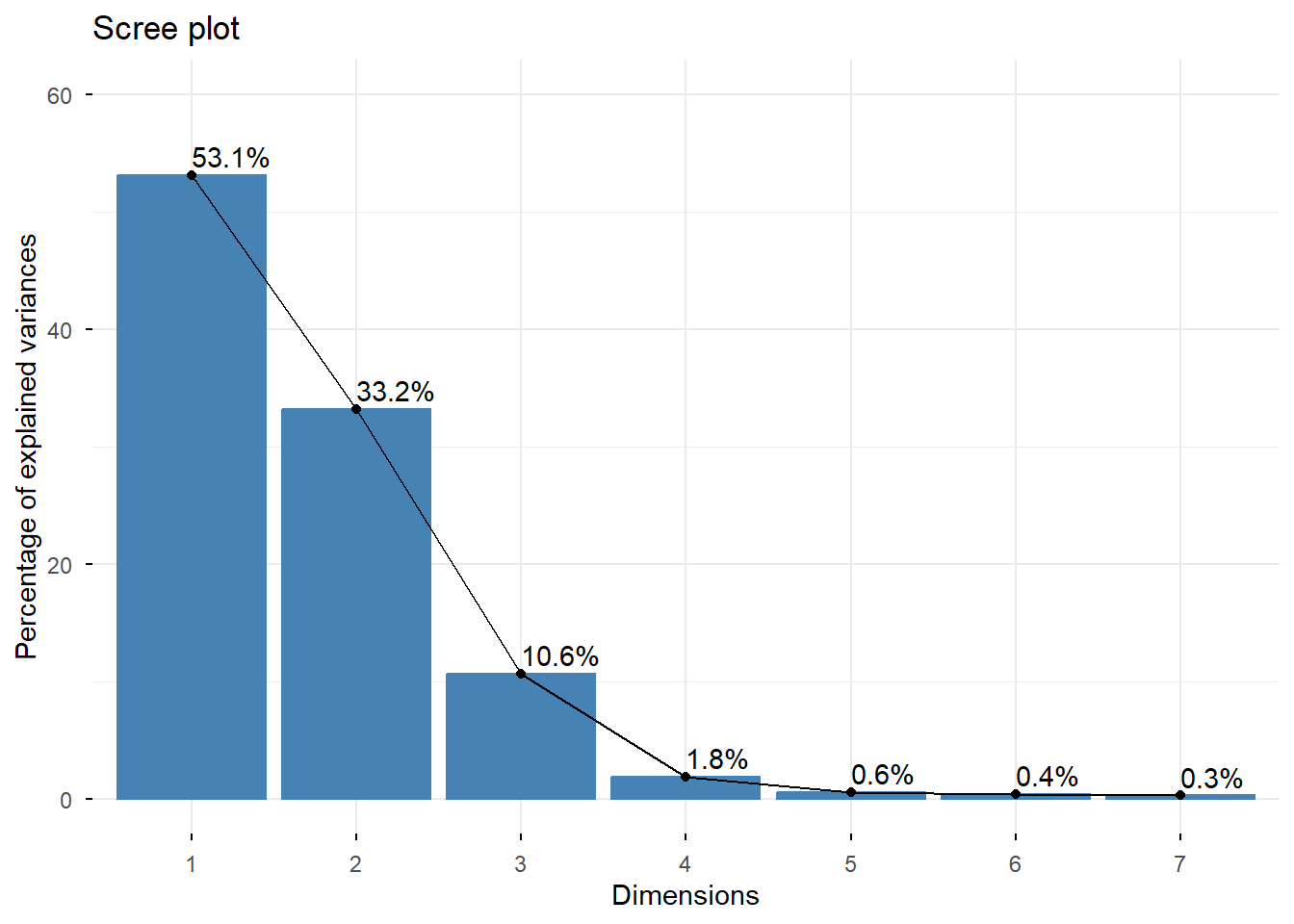
Interpretación: Las dos primeras dimensiones capturan un 86.3% de la inercia total (53.1% + 33.2%). Este es un porcentaje muy alto, lo que significa que nuestro mapa 2D será una representación bastante fiel de las relaciones originales en la tabla.
4.8 4. El Mapa Perceptual: Interpretación del Biplot
El biplot es el resultado principal del ANACO. Muestra las categorías de filas (atributos) y columnas (empresas) en el mismo espacio bidimensional.
# Creamos el biplot simétrico
fviz_ca_biplot(res_ca, repel = TRUE) +
labs(title = "Mapa Perceptual de HATCO y sus Competidores")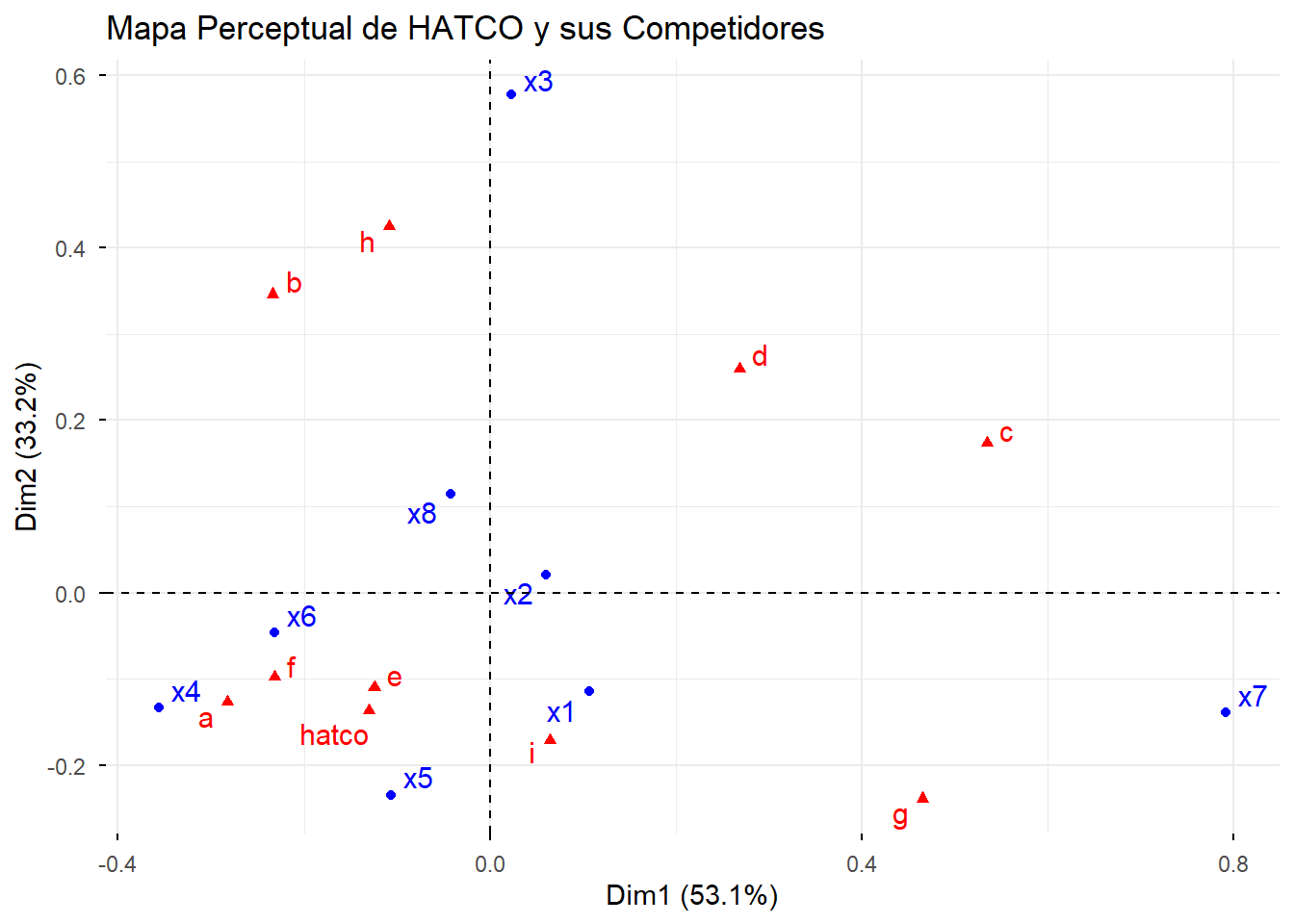
4.8.1 El Decálogo de Interpretación
Para leer el mapa correctamente, sigamos una serie de reglas (basadas en el decálogo de la diapositiva 26):
- Proximidad entre puntos del mismo tipo:
- Empresas: Las empresas que están cerca en el mapa (ej. HATCO, A, F, E) son percibidas de manera similar por los clientes. Compiten directamente.
- Atributos: Los atributos cercanos (ej. x1, x6, x4) tienden a aparecer juntos.
- Asociación entre puntos de diferente tipo (Empresa-Atributo):
- Un atributo que se encuentra cerca de una empresa indica una fuerte asociación. Por ejemplo, la empresa C está fuertemente asociada con el atributo x3 (Flexibilidad de precios). La empresa H está muy asociada con x7 (Calidad del producto).
- Distancia del Origen (Baricentro):
- Los puntos más alejados del origen (0,0) son los que tienen perfiles más distintivos y contribuyen más a la estructura de los datos. Por ejemplo, x7, x3, y las empresas C, G y H son muy discriminantes.
- Los puntos cercanos al origen tienen perfiles “promedio” y son menos característicos.
- Interpretación de los Ejes (Dimensiones):
- Dimensión 1 (Eje Horizontal, 53.1%): Observando los extremos, este eje parece oponer a las empresas de la izquierda (como C y G) con las de la derecha (como A, F, E). El atributo x7 (Calidad) tira fuertemente hacia la izquierda, mientras que x4 (Imagen del fabricante) y x6 (Imagen de los vendedores) tiran hacia la derecha. Podríamos interpretar este eje como “Calidad del Producto vs. Imagen de Marca/Ventas”.
- Dimensión 2 (Eje Vertical, 33.2%): Este eje opone a x3 (Flexibilidad de precios) en la parte superior con x5 (Calidad del servicio) y otros en la inferior. Podríamos llamarlo “Flexibilidad de Precios vs. Calidad de Servicio”.
4.9 5. Profundizando: Calidad (COS2) y Contribuciones
¿Podemos confiar en la posición de todos los puntos del mapa? ¿Qué puntos son los más importantes para definir los ejes?
4.9.1 Calidad de Representación (COS2)
El COS2 (coseno al cuadrado) mide qué tan bien está representado un punto en el mapa 2D. Un valor cercano a 1 significa que la posición del punto en el mapa es muy fiable. Un valor bajo significa que gran parte de su información se encuentra en otras dimensiones no visualizadas.
# Visualizamos la calidad de representación de filas y columnas
fviz_cos2(res_ca, choice = "row", axes = 1:2)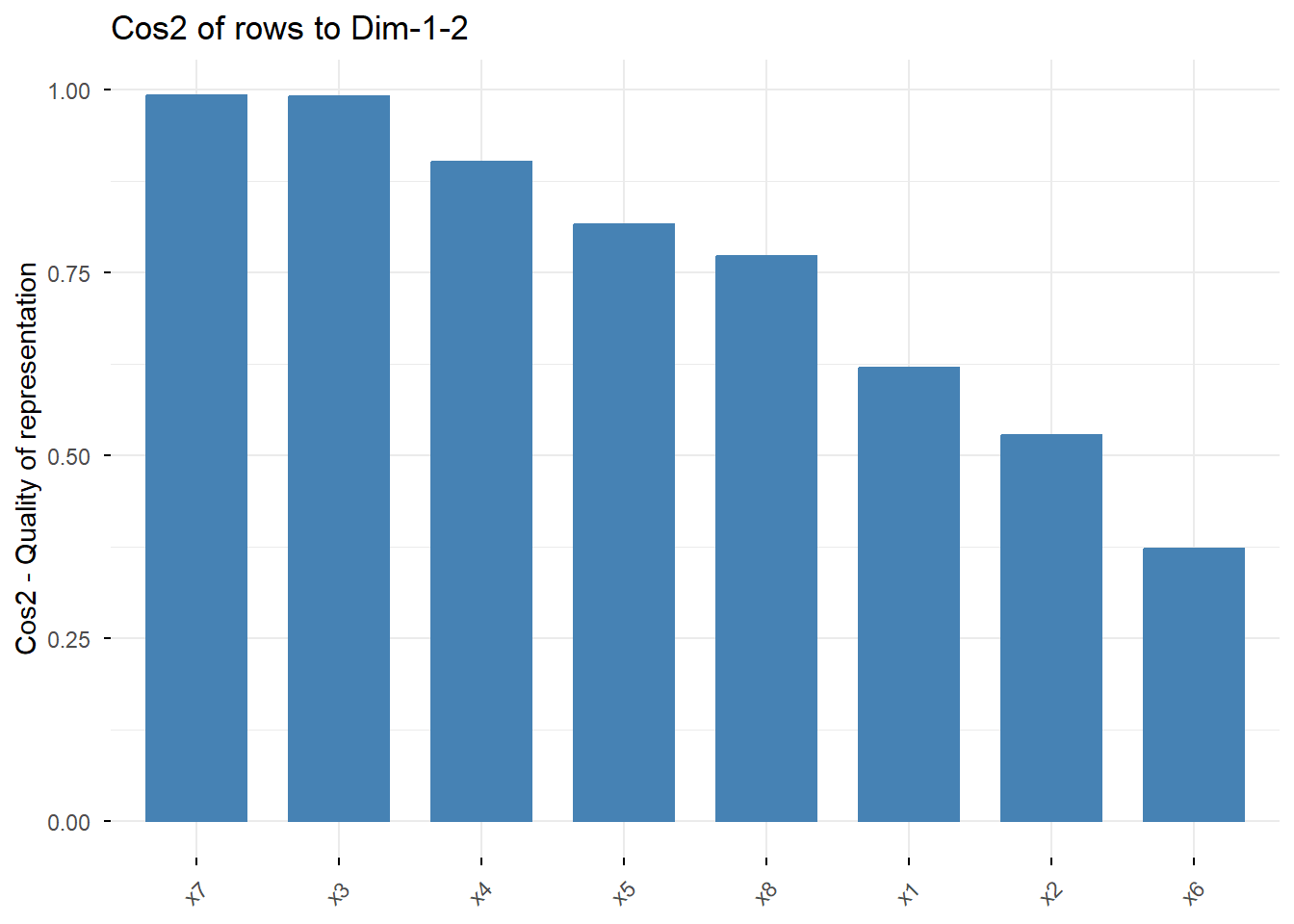
fviz_cos2(res_ca, choice = "col", axes = 1:2)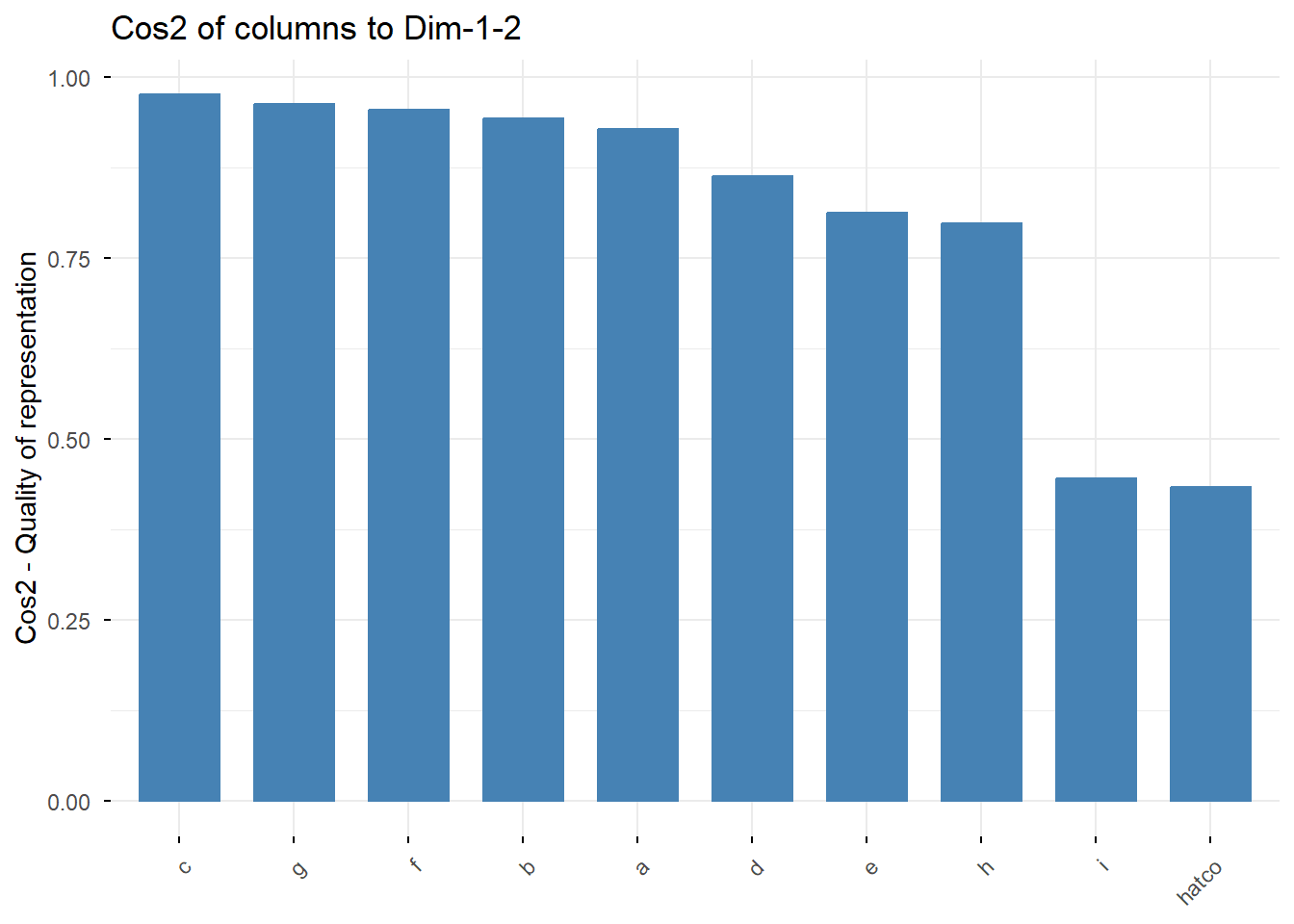
# También podemos colorear el biplot según el COS2
fviz_ca_biplot(res_ca, repel = TRUE, col.row = "cos2", col.col = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07")) +
labs(title = "Biplot Coloreado por Calidad de Representación (COS2)")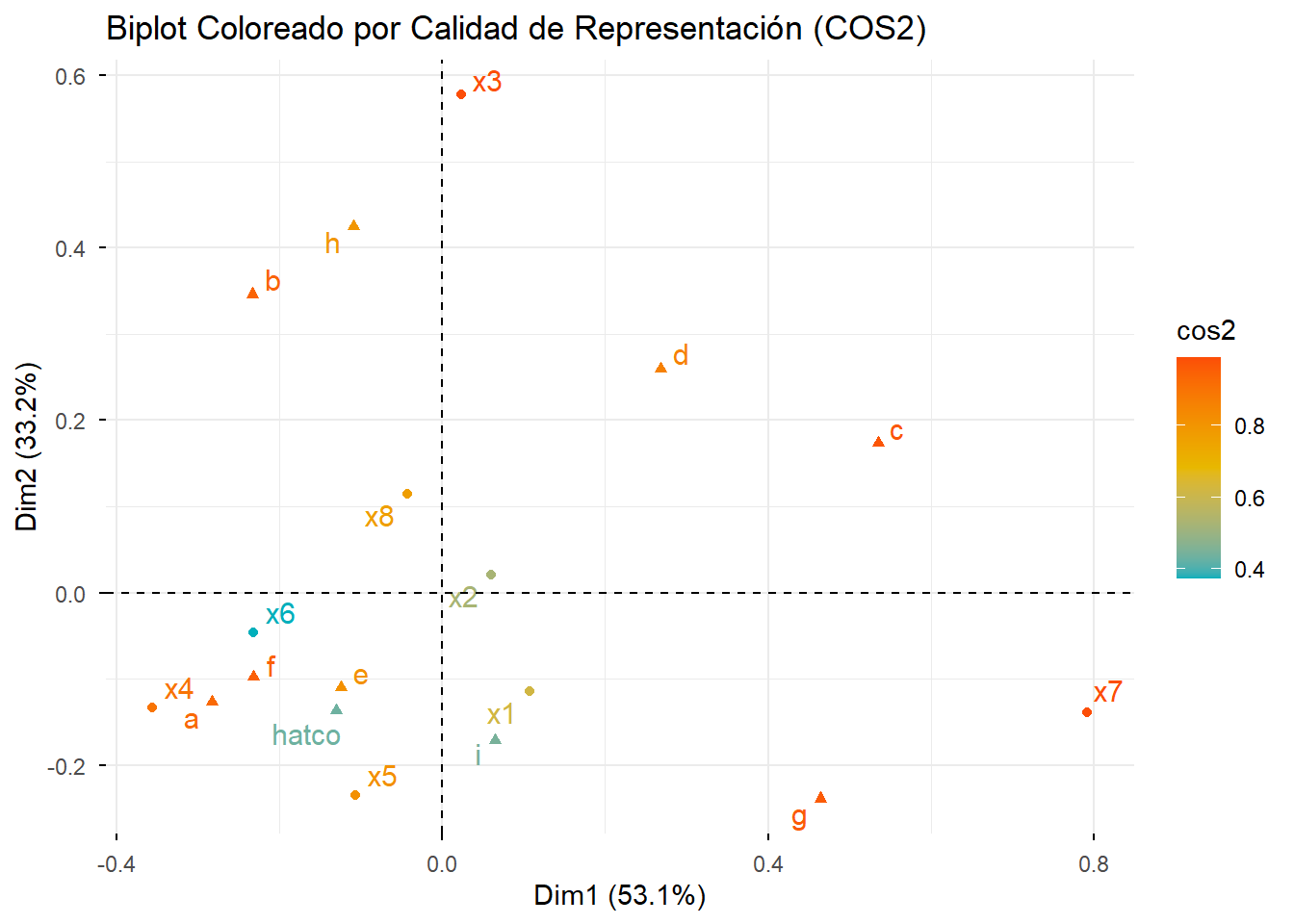
Interpretación: Los puntos con colores más cálidos (naranja/rojo) están mejor representados. Vemos que casi todos los puntos tienen una alta calidad, lo que da confianza a nuestro mapa.
4.9.2 Contribución de los Puntos a las Dimensiones
La contribución nos dice qué puntos son los que más pesan en la definición de cada eje.
# Contribución de filas y columnas a la Dimensión 1
fviz_contrib(res_ca, choice = "row", axes = 1)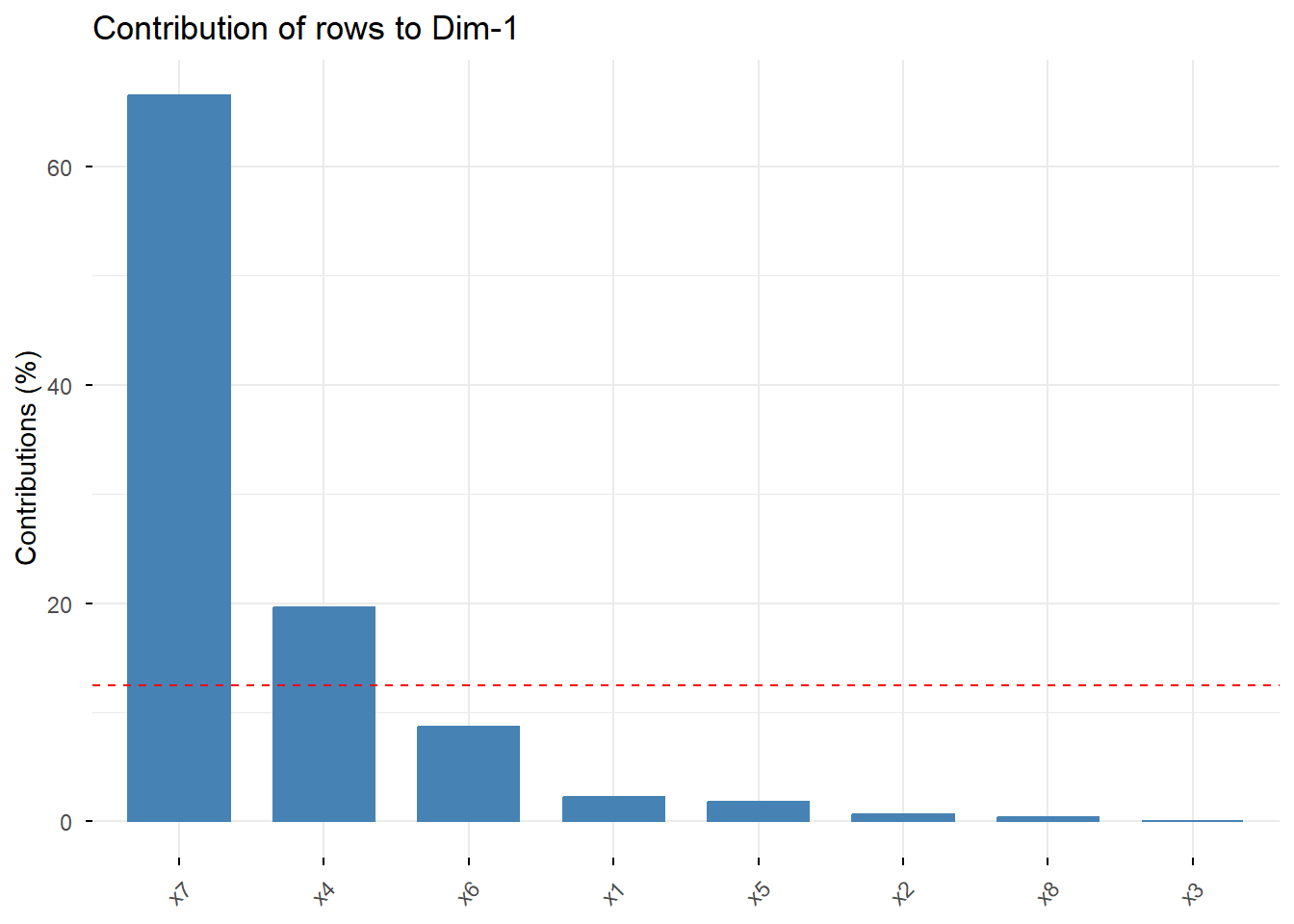
fviz_contrib(res_ca, choice = "col", axes = 1)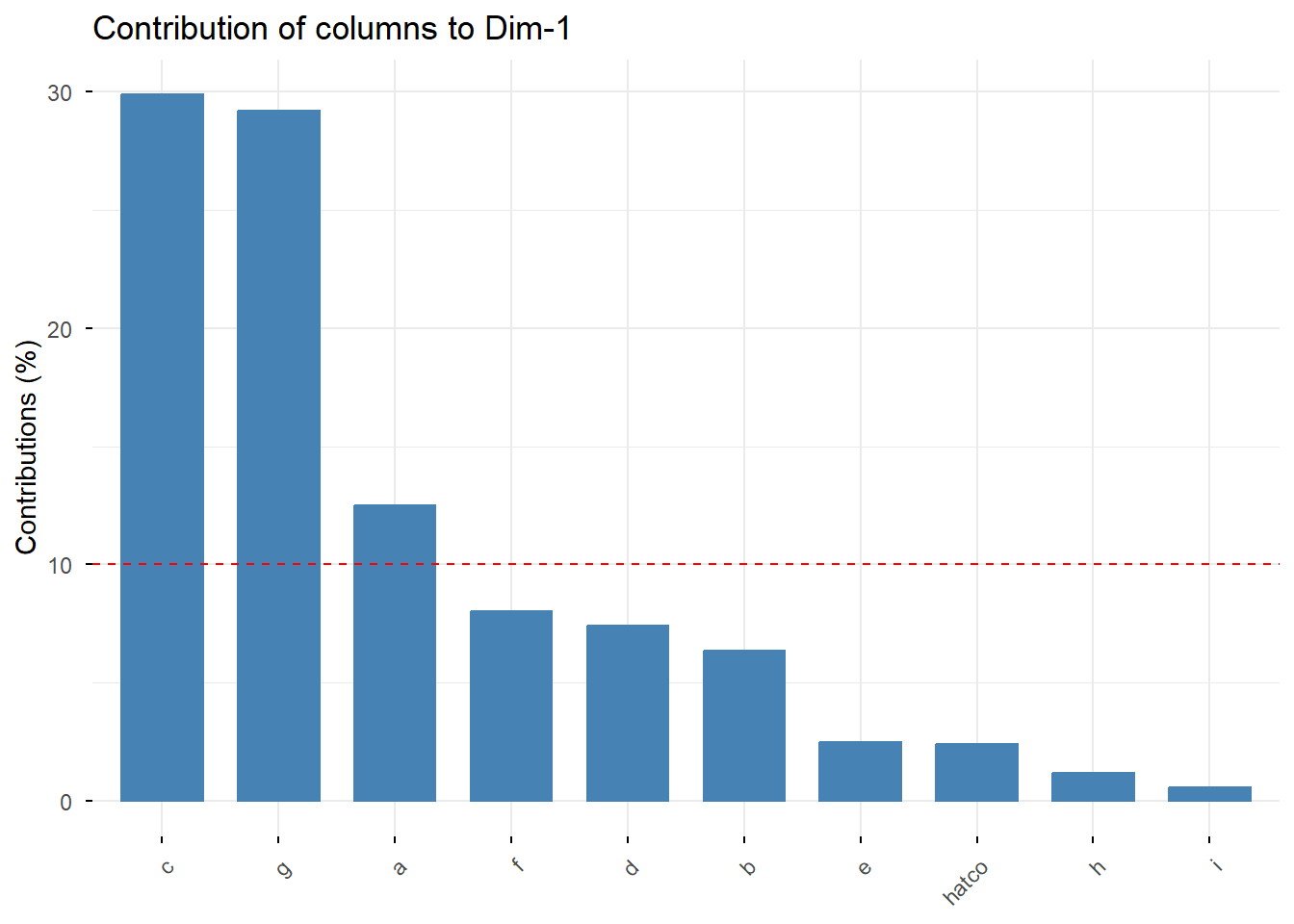
# Contribución de filas y columnas a la Dimensión 2
fviz_contrib(res_ca, choice = "row", axes = 2)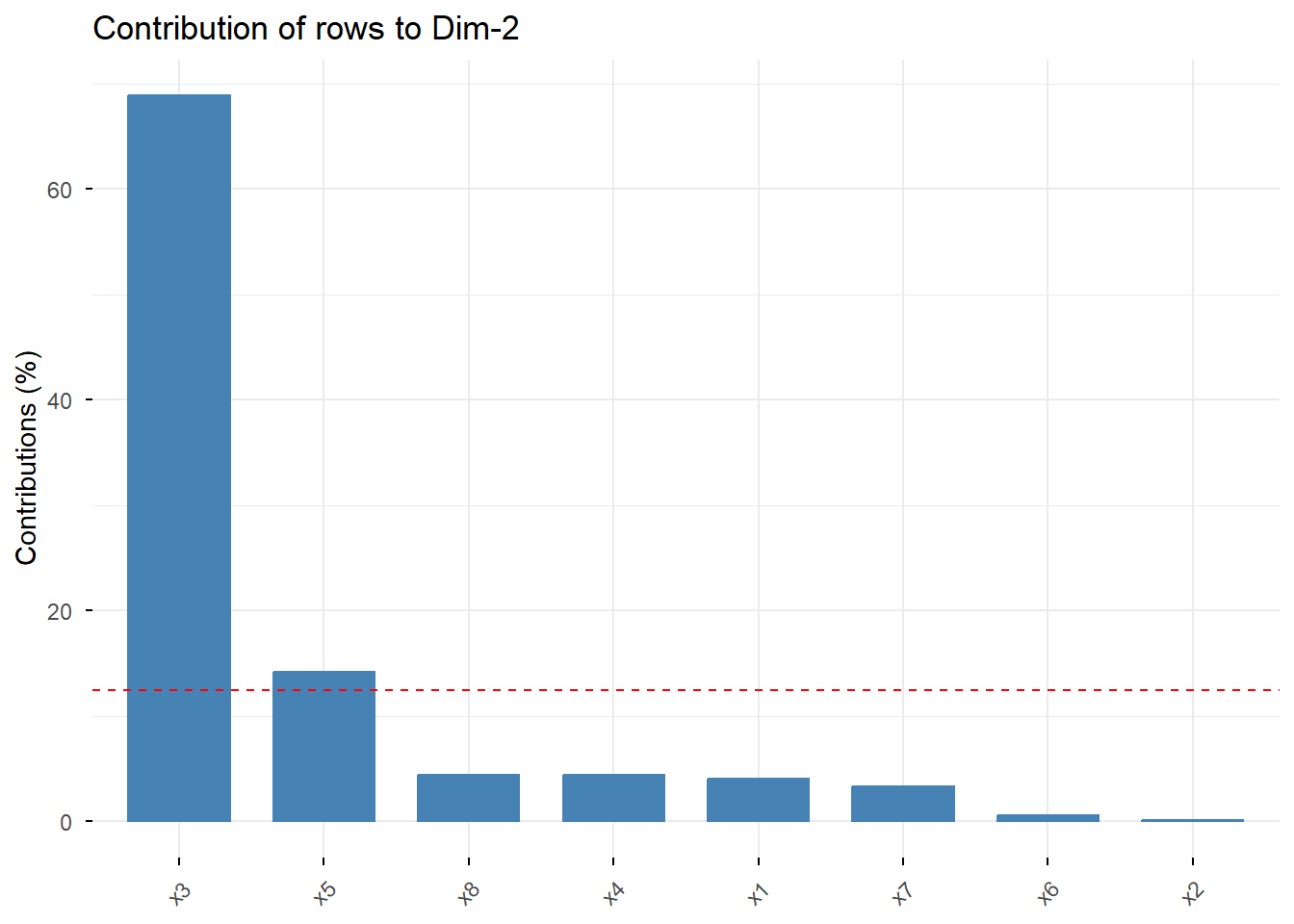
fviz_contrib(res_ca, choice = "col", axes = 2)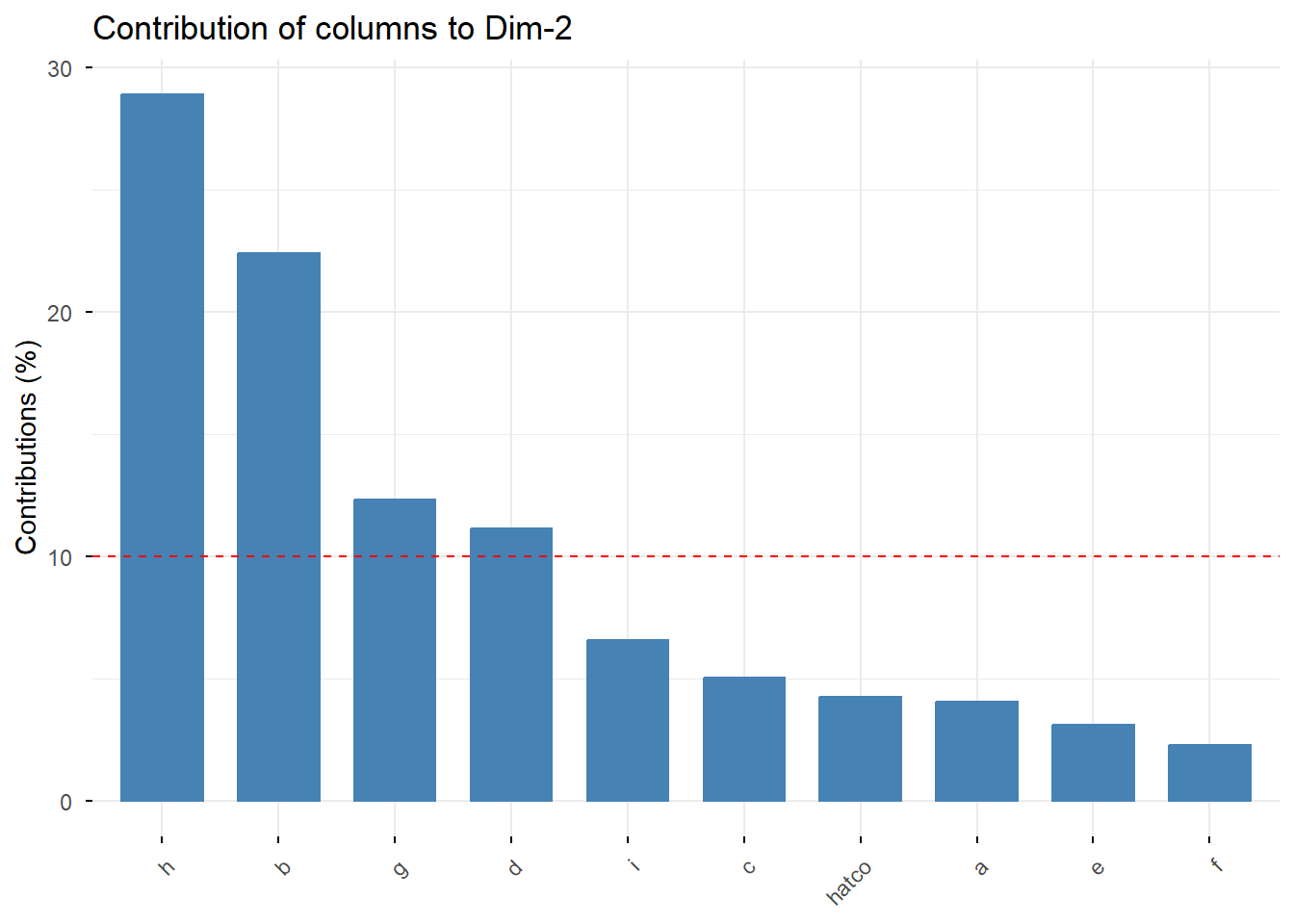
Interpretación: Como vimos antes, x7 (Calidad del producto) y las empresas C y G son los principales contribuyentes a la Dimensión 1. Para la Dimensión 2, el atributo x3 (Flexibilidad de precios) y la empresa B son los más importantes. Esto confirma nuestra interpretación de los ejes.
4.10 6. Elementos Suplementarios
Una de las grandes ventajas del ANACO es la capacidad de añadir elementos “suplementarios”. Estos son puntos (filas o columnas) que queremos proyectar en el mapa para ver dónde se sitúan, pero sin que influyan en la construcción del mapa.
Ejemplo: Añadimos un competidor “IDEAL” que puntúa alto en todos los atributos.
# Creamos la nueva columna para la tabla original
ideal_col <- data.frame(IDEAL = rep(15, 8))
# La añadimos a nuestra tabla
tabla_hatco_sup <- bind_cols(tabla_hatco_ca, ideal_col)
# Volvemos a ejecutar el ANACO, indicando que la columna 11 es suplementaria
res_ca_sup <- CA(tabla_hatco_sup, col.sup = 11, graph = FALSE)
# Visualizamos el nuevo mapa
fviz_ca_biplot(res_ca_sup, repel = TRUE) +
labs(title = "Mapa Perceptual con Competidor 'IDEAL' Suplementario")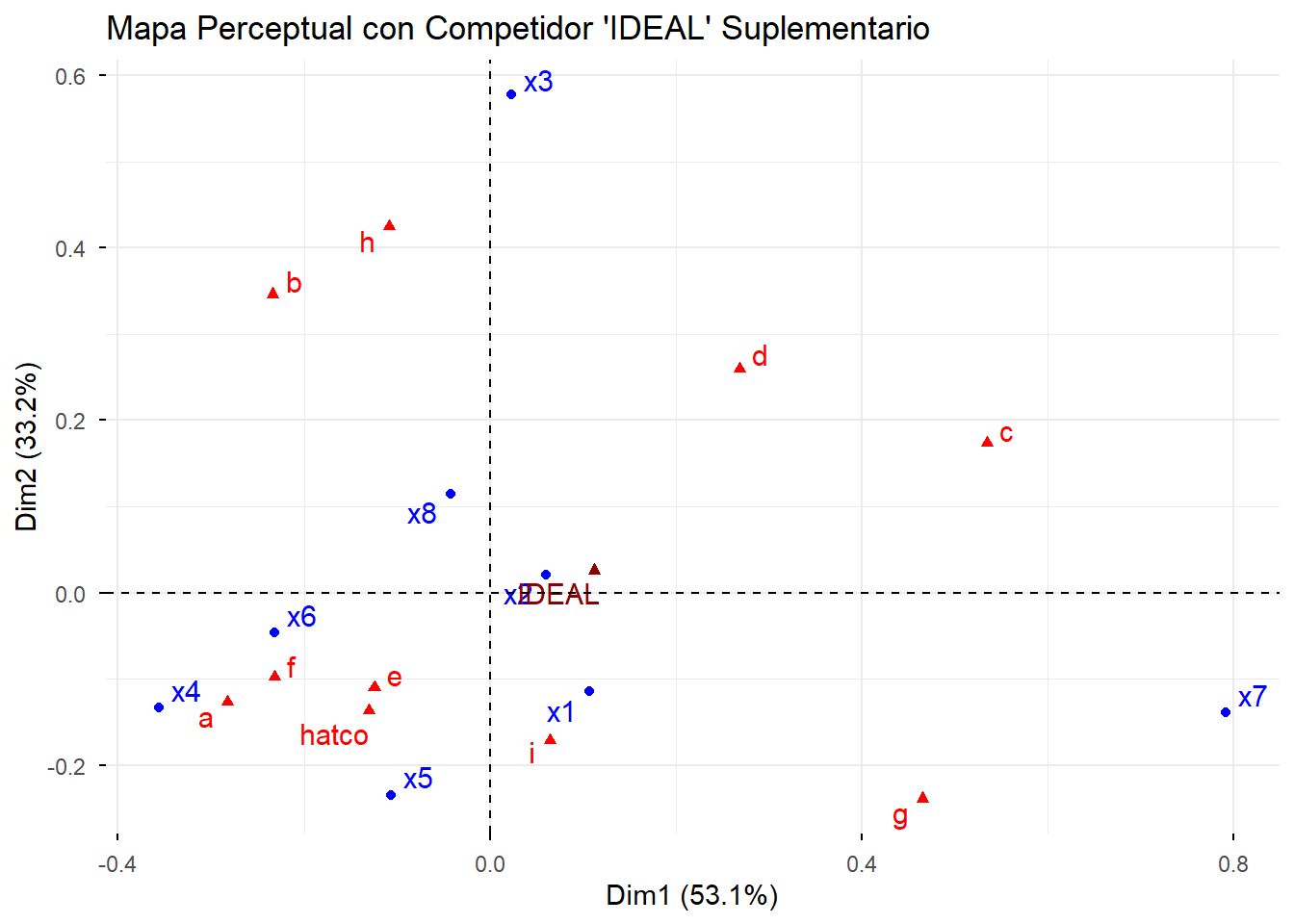
Interpretación: El competidor “IDEAL” se sitúa muy cerca del baricentro, por lo que con esos datos, parece no ser muy buen indicador. Juega con otros valores y analiza los resultados.